Question

How do you graph and solve $|4x+1|\ge 5$ ?

Answer 1

In this question, we have to find the value of x. It is given that there is an inequation; therefore, we did not get the exact answer of x but will get some range where the values of x lie. Thus, we solve this problem using basic mathematical rules. We first remove the absolute sign in the inequation, and thus we get two new inequations. So, we will solve both the inequation separately and thus two different ranges of x. After that, we will draw the graph of the given inequation, to get the required result for the problem.

Complete step-by-step solution:
According to the problem, we have to find the value of x.
The inequation given to us is $|4x+1|\ge 5$ ---------- (1)
Now, we first remove the absolute sign by using the absolute value function property A=\left\\{ \begin{aligned} & -A;A<0 \\\ & A;A\ge 0 \\\ \end{aligned} \right\\} , we get
$(4x+1)\ge 5$ ------- (2)
$(4x+1)<-5$ --------- (3)
So, we will first solve equation (2), which is
$(4x+1)\ge 5$
Now, we will subtract 1 on both sides in the above equation, we get
$4x+1-1\ge 5-1$
As we know, the same terms with opposite signs cancel out each other, we get
$4x\ge 4$
Now, we will divide 4 on both sides in the above equation, we get
$\dfrac{4}{4}x\ge \dfrac{4}{4}$
On further simplification, we get
$x\ge 1$
Therefore, x will take all those values which are greater than or equal to 1, which are 1,2,3.. so on
So, we will first solve equation (3), which is
$(4x+1)<-5$
Now, we will subtract 1 on both sides in the above equation, we get
$4x+1-1<-5-1$
As we know, the same terms with opposite signs cancel out each other, we get
$4x<-6$
Now, we will divide 4 on both sides in the above equation, we get
$\dfrac{4}{4}x<-\dfrac{6}{4}$
On further simplification, we get
$x<-\dfrac{3}{2}$
Therefore, x will take all those values which are lesser than $-\dfrac{3}{2}$ , which are -2,-3,-4,… so on
Thus, the graph for the equation $|4x+1|\ge 5$ is:

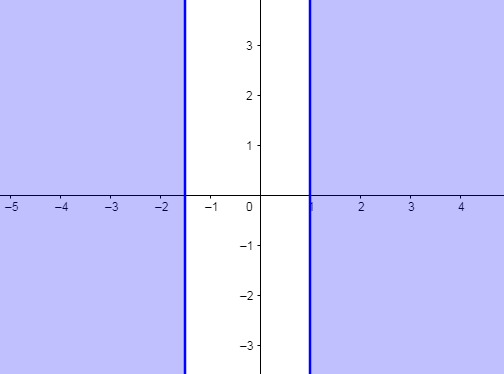
Thus, we see that the shaded region is the region for the equation $|4x+1|\ge 5$ at value of $x\ge 1$ and $x <-\dfrac{3}{2}$.

Note: While solving this problem, do mention all the formulas you are using to avoid confusion and mathematical errors. Do remember how to remove the absolute function. Also, at the end of the solution, we get two different answers, so accordingly draw the graph.