Question

How do you graph and list the amplitude, period, phase shift for $y = - \sin \left( {x - \pi } \right)$ ?

Answer 1

Hint : First, using the suitable trigonometric identities, simplify the given equation and try to get a simplest form of the equation so that we can understand it better. Then find the maximum value of the function.

Complete step by step solution:
The given equation is $y = - \sin \left( {x - \pi } \right) - - - - - - - - - \left( 1 \right)$
This is a trigonometric equation. All trigonometric functions are periodic. This means that the function repeats itself after a regular interval on the Cartesian plane.
The trigonometric function $\sin x$ has a period of $2\pi$ radians. This means that the values of the function $\sin x$ repeat after every interval of $2\pi$ radians.
This helps in graphing the curve of a trigonometric function. We can graph the function for an interval of $2\pi$ radians and then just replicate the function for every such successive interval.
Let us simplify equation $1$ by using the identity $- \sin \theta = \sin \left( { - \theta } \right)$ .
Then,
$\Rightarrow y = - \sin \left( {x - \pi } \right)$
$\Rightarrow y = \sin \left[ { - \left( {x - \pi } \right)} \right]$
$\Rightarrow y = \sin \left( {\pi - x} \right)$
Now, we shall use the identity $\sin \left( {\pi - x} \right) = \sin x$
So, we get, $y = - \sin \left( {x - \pi } \right) = \sin x$
This means that the graph of equation $\left( 1 \right)$ is the same as the graph of trigonometric function $\sin x$ .
So, we get the graph of $y = - \sin \left( {x - \pi } \right)$ as

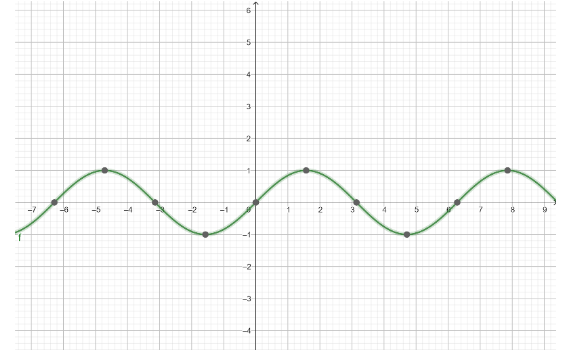
So, we now know that $y = - \sin \left( {x - \pi } \right) = \sin x$
Hence, the maximum value of the function $y = - \sin \left( {x - \pi } \right)$ is $1$ .
Therefore, the amplitude of the function $y = - \sin \left( {x - \pi } \right)$ is $1$ .
Period of the function $y = - \sin \left( {x - \pi } \right)$ is $2\pi$ radians.
Phase shift of the graph is zero.

Note : If we have an equation $A\sin \left( {kx - \phi } \right)$ , then A is the amplitude, $\dfrac{{2\pi }}{k}$ is the period and $\phi$ is the phase shift of the graph.
Here, in this case, $A = 1$ , $k = 1$ and $\phi = 0$ .
This means that amplitude of the function is $1$ , period is $2\pi$ and phase shift is zero.