Question

How do you graph and label the vertex and axis of symmetry of $y=-3{{\left( x-2 \right)}^{2}}+2$

Answer 1

Now the given equation is an equation of parabola in the form $y=a{{\left( x-h \right)}^{2}}+k$ . Now we know that the vertex of parabola in the equation is given by $\left( h,k \right)$ and the axis of symmetry is given by $x=h$ . Also we know that is a > 0 then the parabola is upwards facing and if a < 0 then the parabola is downwards facing.

Complete step by step solution:
Now first consider the given expression $y=-3{{\left( x-2 \right)}^{2}}+2$
Now we know that the given equation is a equation of parabola of the form $y=a{{\left( x-h \right)}^{2}}+k$
Now for the equation of parabola in the form $y=a{{\left( x-h \right)}^{2}}+k$ the vertex of the parabola is given by $\left( h,k \right)$ .
Now comparing the equation $y=-3{{\left( x-2 \right)}^{2}}+2$ with $y=a{{\left( x-h \right)}^{2}}+k$ we get h = 2 and k = 2.
Hence the vertex of the parabola is $\left( 2,2 \right)$ .
Now here $a = -3$. Since a is negative we have that the parabola is downwards facing.
Now let us understand the meaning of the axis of symmetry. Now the axis of symmetry is a line which cuts the parabola in two equal parts.
Now we know that if $\left( h,k \right)$ is the vertex of the parabola then x = h will be the axis of symmetry of the parabola.
Hence we get that the axis of symmetry of the given parabola is $x=2$ .
Hence the given parabola is a downwards facing parabola with its axis of symmetry as x = 2 and vertex as $\left( 2,2 \right)$ .
Now let us draw the graph of the parabola.

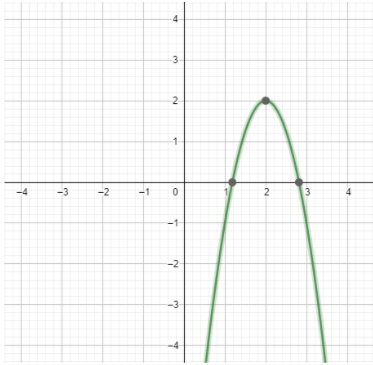
Note: Now note that we can also write the given equation in general quadratic form of the expression which is $a{{x}^{2}}+bx+c$ . Now we know that if a is negative then the parabola is downwards facing and the vertex in this case is $\left( \dfrac{-b}{2a},f\left( \dfrac{-b}{2a} \right) \right)$ . Hence we can plot the graph of the function. Note that we can also find the vertex by using the condition $f'\left( x \right)=0$ .