Question

How do you graph an ellipse written in general form?

Answer 1

We first explain the general form of an ellipse as $\dfrac{{{\left( x-\alpha \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-\beta \right)}^{2}}}{{{b}^{2}}}=1$. We try to find the form of $\dfrac{\overline{SP}}{\overline{PM}}=e$ where $0 < e < 1$. We then find the coordinates of foci, vertices, centre to plot the equation of the ellipse in the graph.

Complete step-by-step answer:
The general form of an ellipse is $\dfrac{{{\left( x-\alpha \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-\beta \right)}^{2}}}{{{b}^{2}}}=1$. Condition being ${{a}^{2}}>{{b}^{2}}$.
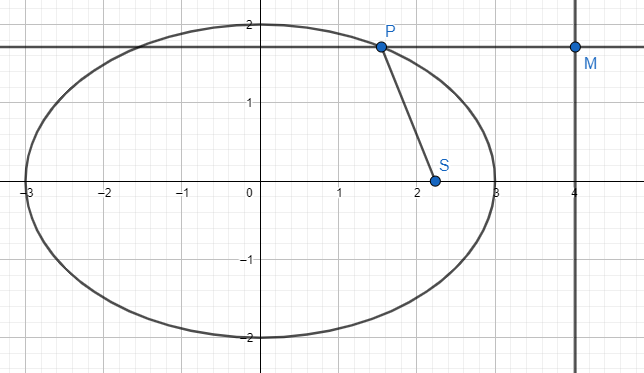
Let us assume an arbitrary point on the ellipse. The point is $p\left( x,y \right)$. S be the focus of the ellipse. M be the foot of the perpendicular of the point $p\left( x,y \right)$ on the directrix of the ellipse.
Therefore, $\overline{SP}$ denotes the distance from point $p\left( x,y \right)$ to the focus and $\overline{PM}$ denotes the distance from point $p\left( x,y \right)$ to the point M.
If $e$ be the eccentricity for the ellipse then $\dfrac{\overline{SP}}{\overline{PM}}=e$. The value of $e$ is $0 < e < 1$.
The ellipse would have two axes. One major and another minor axis.
The length of the major and minor axes is $2a$ and $2b$ units.
The coordinates of the centre are $\left( \alpha ,\beta \right)$ and the coordinates of vertices is $\left( \alpha \pm a,\beta \right)$.
The eccentricity $e$ can be represented as $e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}$.
The coordinates of foci are $\left( \alpha \pm ae,\beta \right)$. The length of the latus rectum is $\dfrac{2{{b}^{2}}}{a}$ unit.
The equation of directrices is $x=\alpha \pm \dfrac{a}{e}$.

Note: The shape of the ellipse changes with the value of a and b. The centre value changes with the change of $\left( \alpha ,\beta \right)$. The eccentricity is different for all types of conic figures. The eccentricity value for parabola and ellipse is $e=1$ and $e>1$ respectively.