Question

How do you graph a polar coordinate?

Answer 1

Hint : In order to graph a polar coordinate ,draw a ray equal to the angular coordinate and mark the radius equal to radial coordinate, the point at which the ray drawn intersects the radius is our required polar coordinate on the cartesian plane.
Formula:
$\sin \left( {A - B} \right) = \sin \left( A \right)\cos \left( B \right) - \sin \left( B \right)\cos \left( A \right)$
$\sin \left( {\pi + \theta } \right) = - \sin \theta$
$\cos \left( {\pi + \theta } \right) = - \cos \theta$

Complete step-by-step answer :
There are two ways to determine a point on a plane, one is by the rectangular coordinates and another is by the Polar Coordinates.
Polar Coordinates $(p,\theta )$ is actually a 2D coordinate system in which every point on the plane is found by a distance $p$ from a reference point and an angle i.e. $\theta$ from a reference direction.
where $p$ is the radial coordinate and $\theta$ is known as the angular coordinate.
To draw a polar coordinate on plane lets have an example and plot a polar coordinate
For example , Let's suppose a polar coordinate $\left( {4,\dfrac{{4\pi }}{3}} \right)$
Radial coordinate = $p\,/\,r = 4$
Angular coordinate $= \theta = \dfrac{{4\pi }}{3}$
First we convert the Angular coordinate into degree
So to convert into degree replace $\pi$ with 180
$\theta = \dfrac{4}{3} \times {180^ \circ } \\\ \theta = {240^ \circ } \;$
Now we’ll draw a line which is ${240^ \circ }$ with respect to x-axis
And taking radius as $r = 4$
The point at which the line intersects the radius =4 is our polar coordinate

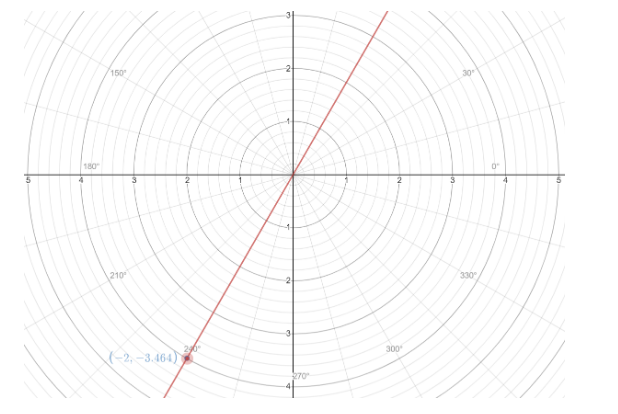
To confirm we have correctly plotted our polar coordinate or not
Let Convert the polar coordinate into rectangular coordinates and if both are same then we can say that we have successfully plotted the polar coordinate correctly
Now to transformation by which we can find our rectangular coordinates
$\left( {x,y} \right)$ is
$x = r\cos \theta \\\ y = r\sin \theta \;$
In our case $r = 4\,and\,\theta = \dfrac{{4\pi }}{3}$
$x = 4\cos \left( {\dfrac{{4\pi }}{3}} \right) \\\ = 4\cos \left( {\pi + \dfrac{\pi }{3}} \right) \;$
Using Allied angle in trigonometry $\cos \left( {\pi + \theta } \right) = - \cos \theta$
$= - 4\cos \left( {\dfrac{\pi }{3}} \right) \\\ = - 4\left( {\dfrac{1}{2}} \right) \\\ = - 2 \;$
Using trigonometric value of $\cos \left( {\dfrac{\pi }{3}} \right) = \dfrac{1}{2}$
$y = 4\sin \left( {\dfrac{{4\pi }}{3}} \right) \\\ = 4\sin \left( {\pi + \dfrac{\pi }{3}} \right) \;$
Using Allied angle in trigonometry $\sin \left( {\pi + \theta } \right) = - \sin \theta$
$= - 4\sin \left( {\dfrac{\pi }{3}} \right) \\\ = - 4\left( {\dfrac{{\sqrt 3 }}{2}} \right) \\\ = - 2\sqrt 3 \;$
Using trigonometric value of $\sin \left( {\dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 3 }}{2}$
Therefore, polar coordinates $\left( {4,\dfrac{{4\pi }}{3}} \right)$ in rectangular coordinates are $\left( { - 2, - 2\sqrt 3 } \right)$ .
And we can see from the graph both points are the same.

Note : 1.One must be careful while taking values from the trigonometric table and cross-check at least once
2.To verify your answer, plot both polar and rectangular coordinates on the cartesian plane and if both are the same then the answer is correct and if they both do not represent the same point then your transformation is wrong ,check your solution.