Question

How‌ ‌do‌ ‌you‌ ‌graph‌ ‌a‌ ‌parabola‌ ‌${{x}^{2}}=4y$?

Answer 1

: Now first we will compare the given equation with the general form of the parabola and hence find the nature of the parabola as well as its coordinate of vertex. Now we will substitute different values of x and find corresponding different values of y so that we get the solution pair (x, y) for the given equation. Now we will plot the points on the graph and then draw a parabola passing through the points and given vertex.

Complete step-by-step solution:
Now consider the given equation of the parabola ${{x}^{2}}=4y$
Since the given equation is a parabola of the form ${{x}^{2}}=4ay$ the parabola is upward facing and the directrix is parallel to the x axis.
Now comparing the given equation to the equation ${{\left( x-h \right)}^{2}}=4a{{\left( y-k \right)}^{2}}$ we get h = k = 0 and a = 1.
Now we know that (h, k) is the coordinates for vertex and a is the distance of origin to focus.
Hence we can say that the vertex of parabola is (0, 0) and the focus of parabola is (0, 1).
Now let us substitute some values of x and find corresponding values of y.
By substituting x = 2 we get y = 1.
By substituting x = - 2 we get y = 1.
Now if we substitute x = 4 or x = - 4 we get y = 4.
Similarly if we substitute x = 6 or – 6 we get y = 9.
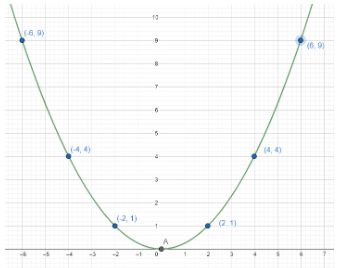
Now plot the points (2, 1), (-2, 1), (4, 4), (4, -4), (6, 9) and (-6, 9).
Now plot the parabola passing through the points such that the vertex of parabola is (0, 0) and the parabola is upwards facing.
Hence we get the graph as,

Note: Note that while plotting the points for the graph always take equal negative and positive points to get a proper structure to draw a curve. Also note that since parabola is symmetric about its axis we will get the same values of y for 2 values of x.