Question

How do you graph $- 6x + 9y = - 18$ ?

Answer 1

We will plot the graph for the equation of line using the intercept form of the equation. We will find the intersection points of line on the graph. The intersection point will satisfy the equation of line. We have to find the intercepts of the line on $x -$axis and $y -$axis. To find the $y -$ intercept of line, substitute $x = 0$in the equation of line and substitute $y = 0$in the equation of line to get $x -$intercept of the line. We will equate the equation of a given line with the equation of general form of line. The general equation of a line having slope of $m$ and intercepts on the coordinate axis $c$ is $y = mx + c$. The slopes of a parallel line are equal and if the two lines are parallel then the slope will be equal and they have different $y -$intercept.

Complete step by step solution:
Step: 1
the given equation of the line is,
$- 6x + 9y = - 18$
Convert the equation of line into standard form of line.
$\Rightarrow y = \dfrac{2}{3}x - 2$
Now compare the given equation of line to find the intercepts of the line.
The standard equation of line is,
$y = mx + c$
Where, $m$ is the slope of the line and $c$ is the $y -$ intercept of the line on the axis.
Therefore the intercept of the given line is $c = - 2$.
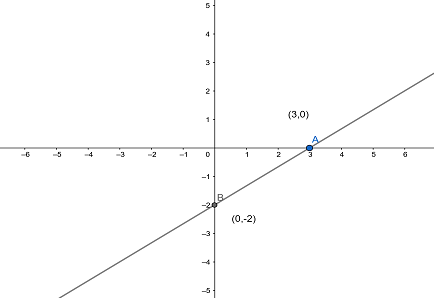
The coordinate of the $y -$intercept of the line is $\left( {0, - 2} \right)$
To find the $x -$intercept of the line, substitute $y = 0$ in the equation of line.
Therefore,
$\Rightarrow \dfrac{2}{3}x - 2 = 0$
Solve the given equation to find the value of $x$ .
$\Rightarrow \dfrac{2}{3}x - 2 = 0 \\\ \Rightarrow x = 3 \\\$
Therefore the $x -$intercept of the line is equal to 3 and the coordinate of the intercept is equal to $\left( {3,0} \right)$.
To plot the graph of the line, mark the $x -$intercept and $y -$intercept of the line on the graph and join them by straight line.

Note:
Plot the equation of line on the graph by finding its intercept made by them on the axis. To find the intercept made by lines on the axis, substitute $x = 0$ and $y = 0$ in the equation of lines. Students are advised to remember the equation of standard line $y = mx + c$ where $m$ is the slope of line and $c$ is the $y -$ intercept of line.