Question

How do you graph $4x = 2y + 6$ using the $x\;{\text{and}}\;y$ intercepts?

Answer 1

Hint : To graph the given equation using intercepts of the axes, first of all you have to find coordinates of both the intercepts and plot both the intercept point on a graph paper then join both the points and then extend the line in order to get the required graph.
Intercepts are calculated by putting the value of one variable zero in the equation to get an intercept of the other and vice versa.

Complete step-by-step answer :
In order to graph the given equation $4x = 2y + 6$ using both intercepts, we will first find the $x\;{\text{and}}\;y$ intercepts by putting value of one of them equals zero and get the other’s intercept and similarly do this process for the other one as follows
Finding $x$ intercept by putting $y = 0$ in the given equation:
$\Rightarrow 4x = 2 \times 0 + 6 \\\ \Rightarrow 4x = 6 \\\ \Rightarrow x = \dfrac{6}{4} = \dfrac{3}{2} \;$
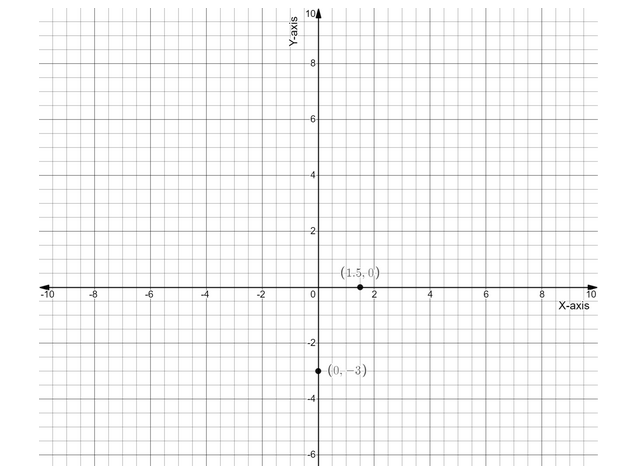
Therefore coordinate of $x$ intercept can be written as $\left( {\dfrac{3}{2},\;0} \right)$
Similarly finding the $y$ intercept, we will get
$\Rightarrow 4 \times 0 = 2y + 6 \\\ \Rightarrow 0 - 6 = 2y \\\ \Rightarrow y = - \dfrac{6}{2} = - 3 \;$
Therefore coordinate of $y$ intercept can be written as $\left( {0,\; - 3} \right)$
Now, plotting these coordinates of intercepts on a graph paper, we will get

Now, joining the points and extending the line we get, then we will get

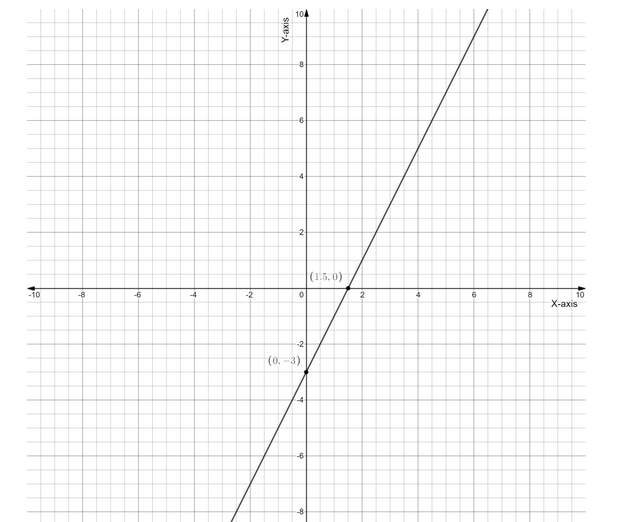
So, this is the required graph for the given equation.

Note : Intercepts method can only be applied or used when the given equation of straight line has intercepts or in other words, the equation which consists of constant term also with the variables have intercepts and so does this method is applicable.