Question

How do you graph $4 - 3i$ in the complex plane?

Answer 1

In order to solve this question, we identify our real number part and imaginary number part and then plot it accordingly on the graph. The x-axis represents the real numbers while the y-axis represents the imaginary numbers.

Complete step-by-step solution:
The given number is $4 - 3i$. This is a mixed number where there are two parts- a complex number and a real number.
Now, we need to plot the given equation on the complex plane. A complex plane is nothing but a Cartesian system containing the standard two axes which is the x-axis and the y-axis. The x- axis represents the real numbers while y-axis represents the imaginary numbers.
Our given number is $4 - 3i$, $4$ represents the real number while $- 3$ is an imaginary number.
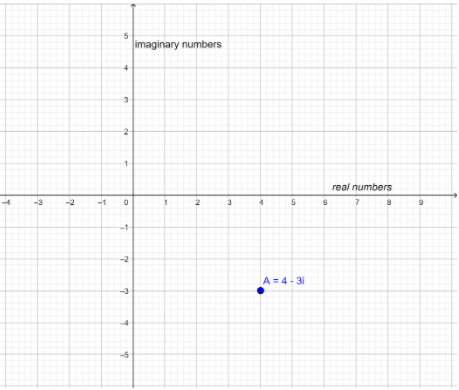
Thus our coordinates are: $\left( {4, - 3} \right)$ where x-coordinate represents the real part and y-coordinate represents the imaginary part.
Plotting this on the graph, we get:
Here point A represents our required coordinate.

Note: A complex number is a number that can be represented as $a + bi$, where a and b are real numbers, and $i$ represents the imaginary unit, satisfying the equation $i = - 1$. Because no real number satisfies the equation, therefore $i$ is called an imaginary number. Some properties of complex numbers are:
When a, b, c and d are real numbers and a+$i$b=c+$i$d, then a=c and b=d
The sum of two conjugate complex numbers is real. For example, if we have a number as $z = a + ib$ , where $a$ and $b$ are real numbers, and the conjugate number $\overline z = a - ib$ , then the sum of $z + \overline z$ is a real number.
The product of two conjugate complex numbers is real.