Question

How do you graph $3x + y = - 2$?

Answer 1

First, we have to make the given linear equation in Slope-intercept form and then calculate the value of $y$ for any two arbitrary values of $x$. Next make a table of these values of $x$ and $y$. Next plot the obtained points on the graph paper and draw a line passing through these points.

Formula used:
Slope Intercept of a line:
The equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.

Complete step by step answer:
Given linear equation in two variables: $3x + y = - 2$
First, we have to make the given linear equation in Slope-intercept form.
So, subtract $3x$ from both sides of the equation.
$y = - 2 - 3x$
Now, we have to calculate the value of $y$ for any two arbitrary values of $x$. Thus, finding the value of $y$ when $x = 0$ and $x = 1$.
When $x = 0$, $y = - 2 - 3 \cdot 0 = - 2$
When $x = 1$, $y = - 2 - 3 \cdot 1 = - 5$
Now we have to make a table of these values of $x$ and $y$.

$x$	$0$	$1$
$y$	$- 2$	$- 5$

Now we have to plot the points $A\left( {0, - 2} \right)$ and $B\left( {1, - 5} \right)$ on the graph paper and draw a line passing through $A$ and $B$.

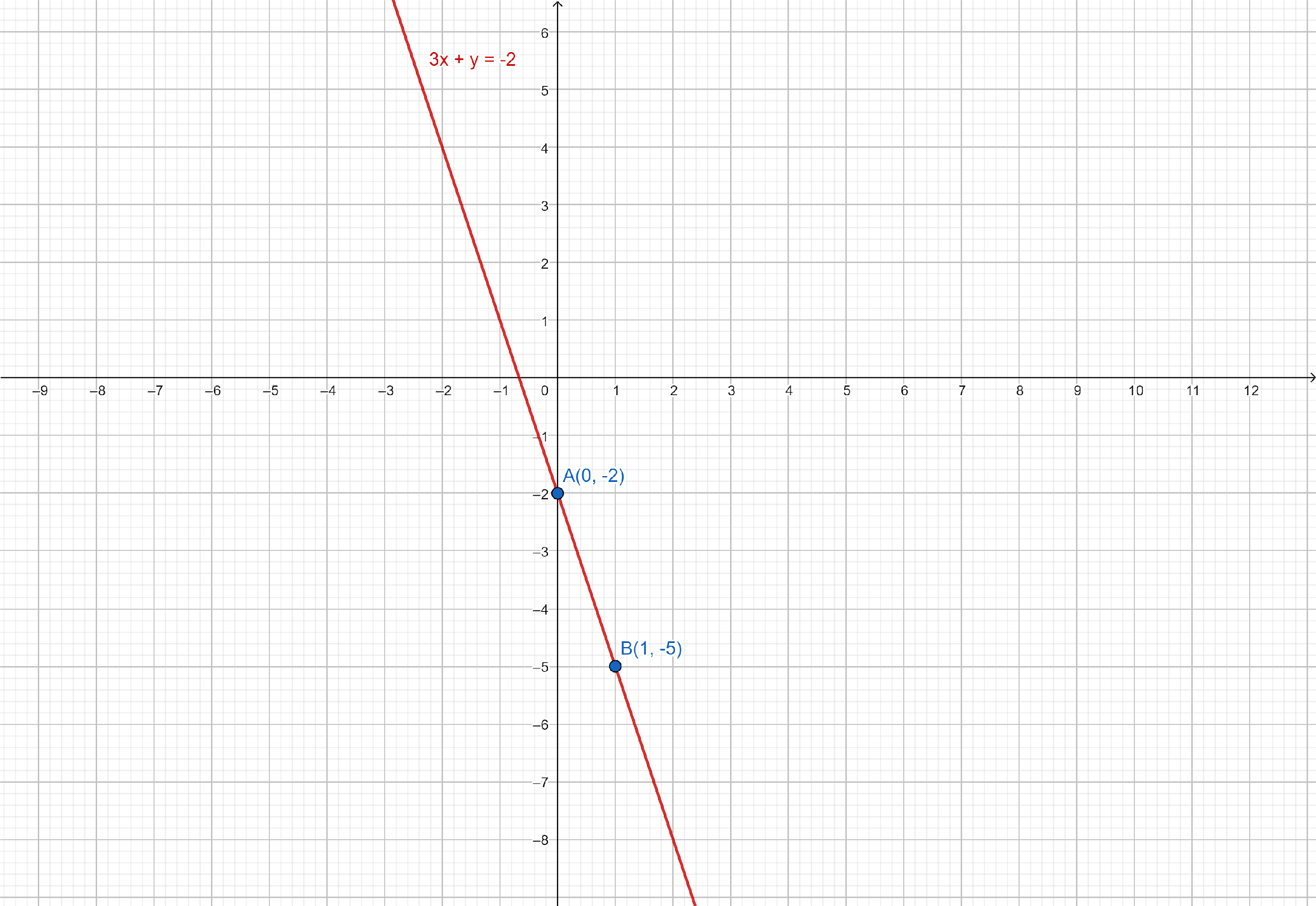
Final solution: Hence, the straight line, so obtained, is the required graph of the given linear equation.

Note: Method to draw the graph of linear equation in two variables:
Step I: Write a given linear equation and express y in terms of x.
Step II: Put different values of x and find the corresponding value of y.
Step III: Form a table by writing the values of y below the corresponding values of x.
Step IV: Plot these points on graph paper.
Step V: Join these points. Thus, we get a straight line and produce it on both sides.
Hence, the straight line, so obtained, is the required graph of the given linear equation.