Question

How do you graph $3x - 4y = 12$?

Answer 1

To draw a graph, we need at least two points which lie on the given line. We can find the two intercepts of the line and use them as the two coordinates to draw that line.

As we know that the two kinds of intercepts are $x$-intercept and $y$-intercept. So, $x$-intercept is the point where the line intersects the $x$-axis and $y$-intercept is the point where the line intersects the $y$-axis.

So, to calculate the intercepts, we will put $x$ and $y$ as zero one by one and then once we get both the intercepts, we will use the coordinates of the intercepts and draw the line on a graph.

Complete step by step solution:
(i)
We are given the line equation:
$3x - 4y = 12$

As we are asked to draw the graph of $3x - 4y = 12$ , we first need to calculate both of the intercepts namely, $x$-intercept and $y$-intercept.

Now, as we know that $x$-intercept is the point where the line crosses the $x$-axis and we also know that on $x$-axis, $y = 0$. Therefore, to find the $x$-intercept, we will put $y$ as $0$ in the equation of line given to us. Therefore,

$3x - 4(0) = 12 \\\ 3x = 12 \\\ x = \dfrac{{12}}{3} \\\ x = 4 \\\$

Therefore, the $x$-intercept of the equation $3x - 4y = 12$ is $4$.

(ii)
Similar to $x$-intercept, $y$-intercept is the point where the line crosses the $y$-axis and we also know that on $y$-axis, $x$=0. Therefore, to find $y$-intercept, we will put $x$ as $0$ in the equation of the line given to us. Therefore,

$3(0) - 4y = 12 \\\ \- 4y = 12 \\\ y = \dfrac{{12}}{{ - 4}} \\\ y = - 3 \\\$

Therefore, the $y$-intercept of the equation $3x - 4y = 12$ is $- 3$.

(iii)
Now, to draw a graph we need two points which lie on the line. As we have calculated both the intercepts, we can say that the line crosses the $x$-axis when $x = 4$ as the $x$-intercept of the given line is $4$ and we also know that on the $x$-axis, $y = 0$. So, we have a point $\left( {4,0} \right)$ which lies on the line $3x - 4y = 12$.

Similarly, the line crosses the $y$-axis when $y = - 3$ as the $y$-intercept of the given line is $- 3$ and we also know that on the $y$-axis, $x = 0$. So, we have another point which lies on the line $3x - 4y = 12$ as $\left( {0, - 3} \right)$.

Marking these two points on a graph and then joining the points through a line will give us the graphical representation of the line $3x - 4y = 12$.

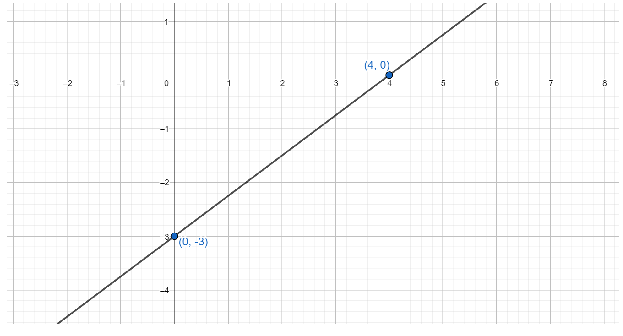
Hence, this is the line $3x - 4y = 12$ drawn on a graph.

Additional Information: A line parallel to $x$-axis, does not intersect the $x$-axis at any finite distance and hence, we cannot get any finite $x$-intercept of such a line. Similarly, lines parallel to the $y$-axis, do not intersect $y$-axis at any finite distance and hence, we cannot get any finite $y$-intercept of such a line.

Note: In an equation of the form $y = mx + c$, $m$ represents the slope of the line and $c$ represents the vertical intercept or $y$-intercept of the line as it is the value of $y$ when $x = 0$.

Also, there is an alternative method to find the intercepts of a line equation. Convert the given line equation into intercept form of a line i.e., $\dfrac{x}{a} + \dfrac{y}{b} = 1$, where $a$ is the $x$-intercept and $b$ is the $y$-intercept.