Question

How do you graph $3x + 2y = 6$ by plotting points?

Answer 1

Hint : In order to graph the above equation, consider the fact the graph to any linear function of the form $ax + by + c = 0$ is always a straight line ..As to plot a straight line we require two points. One point is the x-intercept obtained by putting $y = 0$ and another is the y-intercept obtained by putting $x = 0$ in the equation. By plotting, these two points and connect them to obtain the straight line of the equation.

Complete step-by-step answer :
We are given a linear equation in two variables $x\,and\,y$ i.e. $3x + 2y = 6$
As we know the graph to a linear function of the form $ax + by + c = 0$ is always a straight line.
So, in order to draw a line, we must have at least two points on the graph which we can connect to form a line.
We’ll be taking one point as y-intercept and another as x-intercept .
To calculate y-intercept of the graph, put $x = 0$ in the equation

$$3x + 2y = 6 \\\ 3\left( 0 \right) + 2y = 6 \\\ 2y = 6 \\\ y = \dfrac{6}{2} \\\ y = 3 \\\$$

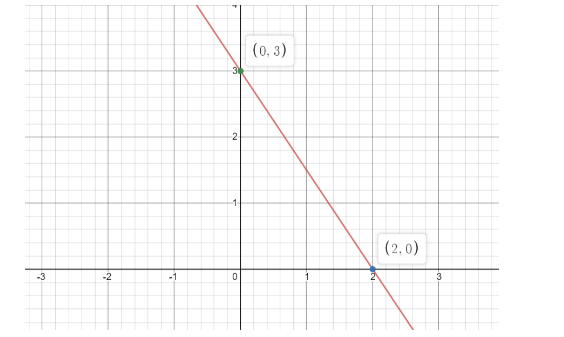
We get y-intercept at point $\left( {0,3} \right)$
Now To calculate x-intercept of the graph, put $y = 0$ in the equation

$$3x + 2y = 6 \\\ 3x + 2\left( 0 \right) = 6 \\\ 3x = 6 \\\ x = \dfrac{6}{3} \\\ x = 2 \;$$

We get x-intercept at point $\left( {2,0} \right)$

X	0	2
y	3	0

Now the graph the equation, we are jumping on the cartesian plan and plot $\left( {0,3} \right)$ , $\left( {2,0} \right)$ .Joining these two points we get a straight line representing our equation $3x + 2y = 6$
Graph of equation having y-intercept as $\left( {0,3} \right)$ and x-intercept as $\left( {2,0} \right)$ .

Note : 1.Draw the cartesian plane only with the help of straight ruler and pencil to get the perfect and accurate results.
2.Mark the points carefully.
3. x-intercept is the point at which the line intersects the x-axis of the plane and similarly y-intercept is the point at which line intersects the y-axis of the plane.