Question

How do you graph $2x+5y=10$ using the slope and the y – intercept?

Answer 1

To graph the above equation $2x+5y=10$ which is a straight line using the slope and the y intercept. First of all, we will put x as 0 in this equation and then solve the equation and hence will find the value of y. This value of y where x is 0 is the y intercept. And then the slope is calculated for the above equation $2x+5y=10$ by dividing the coefficient of x to the coefficient of y and then put a negative sign. Now, after that we will plot the y intercept on the graph and equate the slope which we have calculated to the division of y intercept to the x intercept. From this division we will get the value of x intercept. And hence, plot the x intercept on the graph.

Complete step by step solution:
The equation given in the above problem which we have to draw on the graph is as follows:
$2x+5y=10$
Now, we are going to substitute x as 0 in the above equation and we get,
$\begin{aligned} & \Rightarrow 2\left( 0 \right)+5y=10 \\\ & \Rightarrow 0+5y=10 \\\ \end{aligned}$
Dividing 5 on both the sides we get,
$\Rightarrow y=\dfrac{10}{5}=2$
From the above, we got the y intercept as 2. And the coordinate of y intercept on the graph will be (0, 2).
Now, we are going to find the slope of the above straight line equation by dividing the coefficient of x to the coefficient of y and then we put the negative sign in front of the division.
$\Rightarrow slope=-\dfrac{2}{5}$
From the slope, we can see that the slope is negative. This means that the angle made by the straight line with x axis is greater than ${{90}^{\circ }}$.
Now, we know that slope in the graph of the straight line is the division of y intercept to the x intercept so equating the absolute value of the slope to the division of y intercept to x intercept we get,
$\Rightarrow \dfrac{2}{5}=\dfrac{y}{x}$
In the above, we have calculated the y intercept as 2 so substituting the y intercept as 2 in the above equation we get,
$\Rightarrow \dfrac{2}{5}=\dfrac{2}{x}$
In the above equation, 2 will be cancelled out in the numerator on both the sides and we get,
$\begin{aligned} & \Rightarrow \dfrac{1}{5}=\dfrac{1}{x} \\\ & \Rightarrow x=5 \\\ \end{aligned}$
This means that the straight line will cut the x axis at 5 units from origin in the positive direction.
Now, plotting y intercept on the graph we get,

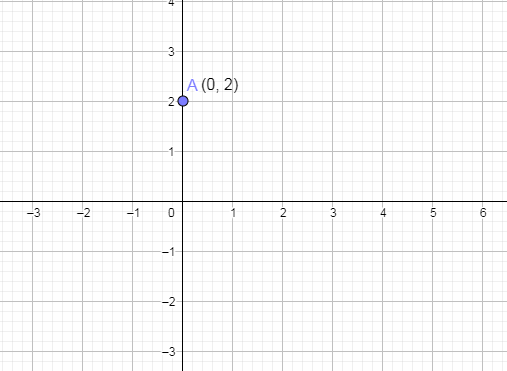
Now, plotting the x intercept on the above graph by marking the point (5, 0) and we get,

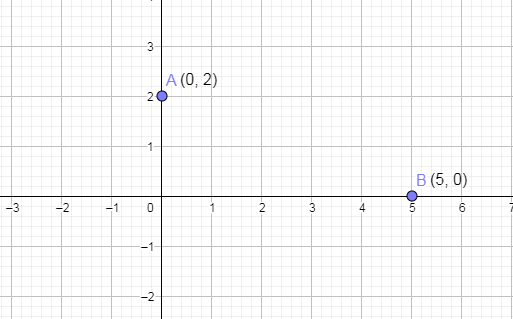
Now, we are going to join these two points A and B and we get,

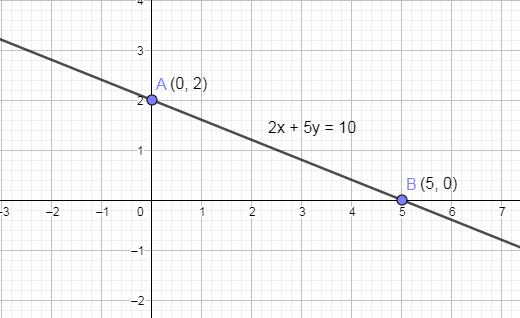
Hence, we have drawn the given straight line.

Note: While finding the x intercept in the above problem, you might think whether the 5 units will be in positive direction or negative direction. So, answer to this question is as the slope we have calculated is negative meaning the angle made by the straight line with x axis is greater than ${{90}^{\circ }}$ and which will occur when the x intercept lies in the positive x direction.