Question

How do you graph $2x+3y=12$?

Answer 1

Change of form of the given equation will give the x-intercept and y-intercept of the line $2x+3y=12$. We change it to the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$ to find the x intercept, and y intercept of the line as $p$ and $q$ respectively. Then we place the points on the axes and from there we draw the line on the graph.

Complete step by step solution:
We are taking the general equation of line to understand the slope and the intercept form of the line $2x+3y=12$.
We change from the equation $2x+3y=12$ to $y=\dfrac{12-2x}{3}=-\dfrac{2}{3}x+4$.
The equation is in the form of $y=mx+k$. m is the slope of the line. The slope of the line is $- \dfrac{2}{3}$.
We have to find the x-intercept, and y-intercept of the line $2x+3y=12$.
For this we convert the given equation into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$. From the form we get that the x intercept, and y intercept of the line will be$p$ and $q$ respectively. The points will be $\left( p,0 \right),\left( 0,q \right)$.
The given equation is $2x+3y=12$. Converting into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$, we get
$\begin{aligned} & 2x+3y=12 \\\ & \Rightarrow \dfrac{2x}{12}+\dfrac{3y}{12}=1 \\\ & \Rightarrow \dfrac{x}{6}+\dfrac{y}{4}=1 \\\ \end{aligned}$
Therefore, the x intercept, and y intercept of the line $2x+3y=12$ is 6 and 4 respectively. The axes intersecting points are $\left( 6,0 \right),\left( 0,4 \right)$.

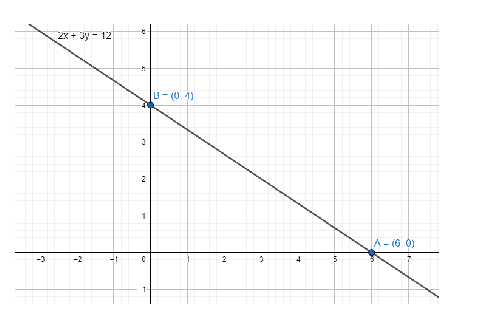
Note: A line parallel to the X-axis does not intersect the X-axis at any finite distance. Hence, we cannot get any finite x-intercept of such a line. Same goes for lines parallel to the Y-axis. In case of slope of a line the range of the slope is 0 to $\infty$.