Question

How do you graph $2{(x - 3)^2} + 2{y^2} = 8$ ?

Answer 1

Hint : We have given an equation as $2{(x - 3)^2} + 2{y^2} = 8$ , we have to reduce it into the standard form of circle. A standard form of circle represented as ${(y - a)^2} + {(x - b)^2} = {r^2}$ , This also represents the locus that is moving at a constant distance ‘r’ from the centre, where $r$ is the length of the radius of the circle and $(a,b)$ is the point which represent the centre of the circle.

Complete step-by-step answer :
It is given that ,
$2{(x - 3)^2} + 2{y^2} = 8$
We have to reduce this into is standard form ,
Therefore, divide by $2$ both the side of the equation, we will get the following result,
${(x - 3)^2} + {y^2} = 4$
We can also express the above equation as ,
${(x - 3)^2} + {y^2} = {2^2}..........(1)$
Now, compare $(1)$ with the standard form of circle represented as ${(y - a)^2} + {(x - b)^2} = {r^2}$ where $r$ is the length of the radius of the circle and $(a,b)$ is the point which represent the centre of the circle. This also represents the locus that is moving at a constant distance ‘r’ from the centre.
Therefore , we get the following result,
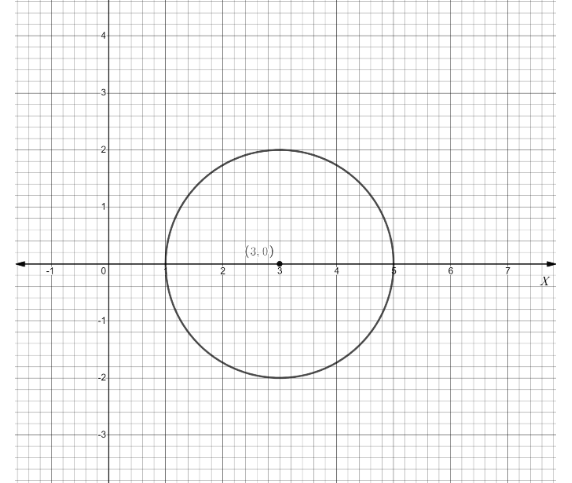
We get the radius of the circle , $r = 2$ and
The coordinate of the circle , $(a,b) = (3,0)$ .
With the help of above data, we can easily draw the required graph as follows

Note : Sometimes the circle equations are given as $a{x^2} + b{y^2} + cx + dy + e = {\text{ }}0$ (in the general form), whenever we have general equation instead of standard one we try to convert the equation in its standard form. So that we can easily get the radius and the respective centre. We can convert it by completing the square rule.