Solveeit Logo
Login

Question

Question: How do you graph \(16{{x}^{2}}+{{y}^{2}}+32x-18y=119\)...

How do you graph 16x2+y2+32x−18y=11916{{x}^{2}}+{{y}^{2}}+32x-18y=119

Explanation

Solution

We equate the given equation of elliptic curve with the general equation of (x−α)2a2+(y−β)2b2=1\dfrac{{{\left( x-\alpha \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-\beta \right)}^{2}}}{{{b}^{2}}}=1. We find the number of x intercepts and the value of the y intercept. We also find the coordinates of the focus and the vertices to place the curve in the graph.

Complete step-by-step solution:
The given equation 16x2+y2+32x−18y=11916{{x}^{2}}+{{y}^{2}}+32x-18y=119 is an elliptic curve.
We convert the equation into a square form and get
16x2+y2+32x−18y=119 ⇒(4x+4)2+(y−9)2=216=(66)2 ⇒(x+1)2(362)2+(y−9)2(66)2=1 \begin{aligned} & 16{{x}^{2}}+{{y}^{2}}+32x-18y=119 \\\ & \Rightarrow {{\left( 4x+4 \right)}^{2}}+{{\left( y-9 \right)}^{2}}=216={{\left( 6\sqrt{6} \right)}^{2}} \\\ & \Rightarrow \dfrac{{{\left( x+1 \right)}^{2}}}{{{\left( \dfrac{3\sqrt{6}}{2} \right)}^{2}}}+\dfrac{{{\left( y-9 \right)}^{2}}}{{{\left( 6\sqrt{6} \right)}^{2}}}=1 \\\ \end{aligned}
We equate (x+1)2(362)2+(y−9)2(66)2=1\dfrac{{{\left( x+1 \right)}^{2}}}{{{\left( \dfrac{3\sqrt{6}}{2} \right)}^{2}}}+\dfrac{{{\left( y-9 \right)}^{2}}}{{{\left( 6\sqrt{6} \right)}^{2}}}=1 with the general equation of parabola (x−α)2a2+(y−β)2b2=1\dfrac{{{\left( x-\alpha \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-\beta \right)}^{2}}}{{{b}^{2}}}=1. We can also see that b2>a2{{b}^{2}}>{{a}^{2}}. The formula changes if b2<a2{{b}^{2}}<{{a}^{2}}.
For the general equation (α,β)\left( \alpha ,\beta \right) is the centre. The vertices are (α,β±a)\left( \alpha ,\beta \pm a \right). The coordinates of the foci are (α,β±be)\left( \alpha ,\beta \pm be \right). Here e=1−a2b2e=\sqrt{1-\dfrac{{{a}^{2}}}{{{b}^{2}}}} is the eccentricity.
This gives the centre as (−1,9)\left( -1,9 \right). The vertices are (−1,9±362)\left( -1,9\pm \dfrac{3\sqrt{6}}{2} \right).
Here e=1−116=154e=\sqrt{1-\dfrac{1}{16}}=\dfrac{\sqrt{15}}{4} is the eccentricity value.
The coordinates of the foci are (−1,9±952)\left( -1,9\pm 9 \sqrt{\dfrac{5}{2}} \right).

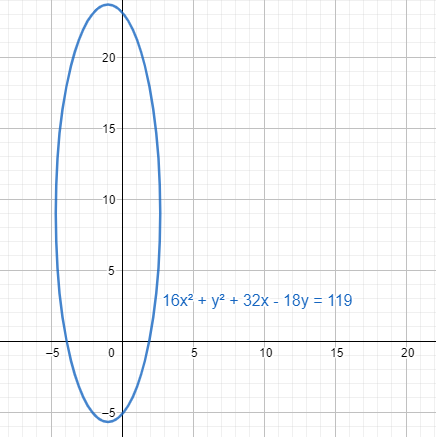
We first find the Y-axis intercepts. In that case for the Y-axis, we have to take the coordinate values of x as 0. Putting the value of x=0x=0 in the equation 16x2+y2+32x−18y=11916{{x}^{2}}+{{y}^{2}}+32x-18y=119, we get
y2−18y−119=0 ⇒y=18±182−4×(−119)×12×1=18±8002=9±102 \begin{aligned} & {{y}^{2}}-18y-119=0 \\\ & \Rightarrow y=\dfrac{18\pm \sqrt{{{18}^{2}}-4\times \left( -119 \right)\times 1}}{2\times 1}=\dfrac{18\pm \sqrt{800}}{2}=9\pm 10\sqrt{2} \\\ \end{aligned}
So, the intercept point for Y-axis is (0,9±102)\left( 0,9\pm 10\sqrt{2} \right).
We find the X-axis intercepts. In that case for X-axis, we have to take the coordinate values of y as 0. Putting the value of y=0y=0 in the equation 16x2+y2+32x−18y=11916{{x}^{2}}+{{y}^{2}}+32x-18y=119, we get

& 16{{x}^{2}}+32x-119=0 \\\ & \Rightarrow x=\dfrac{-32\pm \sqrt{{{32}^{2}}-4\times \left( -119 \right)\times 16}}{2\times 16}=\dfrac{-32\pm \sqrt{8640}}{32}=\dfrac{-4\pm 3\sqrt{15}}{4} \\\ \end{aligned}$$ **The intercept point for X-axis is $$\left( \dfrac{-4\pm 3\sqrt{15}}{4},0 \right)$$.** **Note:** The minimum point of the function $16{{x}^{2}}+{{y}^{2}}+32x-18y=119$ is $\left( -1,9-\dfrac{3\sqrt{6}}{2} \right)$. The graph is bounded at that point. But on the other side the curve is open and not bounded. The general case of parabolic curve is to be bounded at one side to mark the vertex.