Question

How do you FOIL $\left( {x - 1} \right)\left( {x + 2} \right)\left( {x - 3} \right)?$

Answer 1

The given question involves the arithmetic operation of addition/ subtraction/ multiplication/ division. We need to know the FOIL method to solve these types of questions. We need to know how to multiply $x$ the term with $x$ term / $x$ term with the constant term/ constant term with constant term to solve the given question.

Complete step by step solution:
The given question is shown below,
$\left( {x - 1} \right)\left( {x + 2} \right)\left( {x - 3} \right) = ? \to \left( 1 \right)$
To solve this question we use the FOIL method. Here F means First, O means Outside, I means inside and L means Last.
In this question, we have three binomials in multiplication. Let’s solve this,
$\left( 1 \right) \to \left( {x - 1} \right)\left( {x + 2} \right)\left( {x - 3} \right) = ?$
First, we have to solve,
\left( {x - 1} \right)$$$$\left( {x + 2} \right)terms.
So, we get

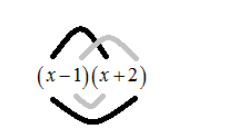
Firsts: $x \times x = {x^2}$
Outsides: $x \times 2 = 2x$
Insides: $- 1 \times x = - x$
Lasts: $- 1 \times 2 = - 2$
So, we get
$\left( {x - 1} \right)\left( {x + 2} \right) = \left( {x \times x} \right) + \left( {x \times 2} \right) + \left( { - 1 \times x} \right) + \left( { - 1 \times 2} \right)$
$\left( {x - 1} \right)\left( {x + 2} \right) = {x^2} + 2x - x - 2$
$\left( {x - 1} \right)\left( {x + 2} \right) = {x^2} + x - 2 \to \left( 2 \right)$
By substituting the equation $\left( 2 \right)$ in the equation $\left( 1 \right)$, we get
$\left( 1 \right) \to \left( {x - 1} \right)\left( {x + 2} \right)\left( {x - 3} \right) = ?$
$\left( {{x^2} + x - 2} \right)\left( {x - 3} \right) = ?$
Let’s follow the FOIL method to the above equation we get

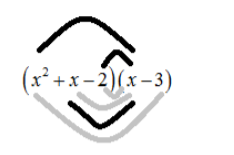
The above figure can be defined by the following table,

| ${x^2}$| $x$| $- 2$
---|---|---|---
$x$| ${x^3}$| ${x^2}$| $- 2x$
$- 3$| $-3{x^2}$| $- 3x$| $6$

So, we get
$\left( {{x^2} + x - 2} \right)\left( {x - 3} \right) = {x^3} - 2{x^2} - 5x + 6$
So, the final answer is,
$\left( {{x^2} + x - 2} \right)\left( {x - 3} \right) = {x^3} - 2{x^2} - 5x + 6$

Note: This question describes the arithmetic equation of addition/ subtraction/ multiplication/ division. Remember the FOIL method to solve these types of questions. Also, remember the following things when we multiply the different sign terms,

1. When a negative number is multiplied with the negative number the answer becomes a
   positive number.
2. When a positive number is multiplied with the positive number the answer becomes a
   positive number.
3. When a negative number is multiplied with a positive number the answer becomes a
   negative number.
   Note that, if the FOIL method is mentioned in the question we would follow the foil method only not using the quadratic formula method to simplify two binomials in multiplication.