Question

How do you find x-intercepts, axis of symmetry, maximum or minimum point, and y-intercept for the equation $y=\dfrac{1}{2}{{\left( x-8 \right)}^{2}}+2$ ?

Answer 1

To find x-intercept, we will put $y=0$ in the given equation. If the roots are real, then the given equation has a x-intercept. To find the axis of symmetry, we will convert the given equation in the form $y=a{{x}^{2}}+bx+c$ . Since, the given equation is of this form, we can see that $y=\dfrac{1}{2}{{\left( x-8 \right)}^{2}}+2$ is a parabola. Then the axis of symmetry will be $x=-\dfrac{b}{2a}$ . Now, we have to check whether a is greater than 0 or not. If a is greater than 0, then the given parabola will have a minimum point. Else, it will have a maximum point. To find this point, convert the given parabola into the form $y=a{{\left( x-h \right)}^{2}}+k$ . Then the vertex of the parabola will be given as $\left( h,k \right)$ . We can find the y-intercept by putting x=0 in the given equation. If the value of y is real, then the given parabola will have y-intercept.

Complete step by step solution:
We need to find x-intercepts, axis of symmetry, maximum or minimum point, and y-intercept for the equation $y=\dfrac{1}{2}{{\left( x-8 \right)}^{2}}+2$ . Let us begin with x-intercept.
We know that x-intercept is a point where the graph of an equation touches the X-axis. In other words, we can say that at x-intercept, $y=0$ . So let us put $y=0$ in the given equation.
$\Rightarrow 0=\dfrac{1}{2}{{\left( x-8 \right)}^{2}}+2$
Let us solve for x.
$\begin{aligned} & \Rightarrow 0-2=\dfrac{1}{2}{{\left( x-8 \right)}^{2}} \\\ & \Rightarrow -2\times 2={{\left( x-8 \right)}^{2}} \\\ & \Rightarrow -4={{\left( x-8 \right)}^{2}} \\\ \end{aligned}$
Taking the square root, we will get
$\begin{aligned} & \Rightarrow 2i=x-8 \\\ & \Rightarrow x=8+2i \\\ \end{aligned}$
We can see that there are no real roots. Therefore, $y=\dfrac{1}{2}{{\left( x-8 \right)}^{2}}+2$ does not have an x-intercept.
Now, let us find the axis of symmetry. We are given that $y=\dfrac{1}{2}{{\left( x-8 \right)}^{2}}+2$ . Let us simplify this equation.
$\begin{aligned} & y=\dfrac{1}{2}\left( {{x}^{2}}-16x+64 \right)+2 \\\ & \Rightarrow y=\dfrac{1}{2}{{x}^{2}}-\dfrac{16x}{2}+\dfrac{64}{2}+2 \\\ & \Rightarrow y=\dfrac{1}{2}{{x}^{2}}-8x+32+2 \\\ & \Rightarrow y=\dfrac{1}{2}{{x}^{2}}-8x+34...(i) \\\ \end{aligned}$
We can see that the above equation is of the form $y=a{{x}^{2}}+bx+c$ . This is an equation of a parabola. We know that, for a parabola, the axis of symmetry is given as
$x=-\dfrac{b}{2a}$ . When we compare the standard form of a parabola to the equation (i), we can see that $a=\dfrac{1}{2},b=-8,c=34$ . Therefore axis of symmetry is given as
$x=-\dfrac{-8}{2\times \dfrac{1}{2}}=8$
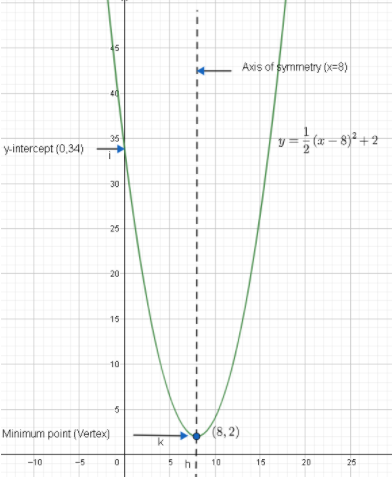
Hence, the axis of symmetry is at x =8.
Now, let us find the maximum or minimum point of the given parabola. This point will be the vertex. To find the vertex, let us consider the standard equation of a parabola in vertex form. This is given as
$y=a{{\left( x-h \right)}^{2}}+k$ . Then the vertex of the parabola will be given as $\left( h,k \right)$ . Let us compare the vertex form to the given equation $y=\dfrac{1}{2}{{\left( x-8 \right)}^{2}}+2$ . We can see that $a=\dfrac{1}{2},h=8,k=2$ .
Therefore, we found the vertex of the parabola to be $\left( 8,2 \right)$ . This is the minimum point since the value of the given parabola is greater than 0 and thus it opens upward.
Now, let us find the y-intercept. We know that y-intercept is the point where the graph of an equation touches the Y-axis. In other words, we can say that at y-intercept, $x=0$ .
Let us substitute this value in the given equation.
$\begin{aligned} & y=\dfrac{1}{2}{{\left( 0-8 \right)}^{2}}+2 \\\ & \Rightarrow y=\dfrac{1}{2}\times 64+2 \\\ & \Rightarrow y=32+2=34 \\\ \end{aligned}$
Hence, the y-intercept will be $\left( 0,34 \right)$ .
Now, let us plot the graph of $y=\dfrac{1}{2}{{\left( x-8 \right)}^{2}}+2$ .

Note: Students must note that a parabola will have x-intercept if the value of x is real when y=0 and y-intercept if the value of y is real when x=0. Also, we can see that when a>0 for a parabola $y=a{{x}^{2}}+bx+c$ , then the parabola will open upward and when a<0, the parabola will open downwards.