Question: How do you find where y and x intersect using a graphing calculator if you have only one proper equa...

Question

How do you find where y and x intersect using a graphing calculator if you have only one proper equation i.e. y = x +2 and x = -3?

Answer 1

Solution

In order to find the intersection point using graphing calculator, we should follow the steps in an order to get the intersection point. First we graph the function that is given in the question then we press TRACE to access the graph of the function. Later we select the intersect option in the calculator and then first the first function and then select the second function. Lastly we move the cursor as close to the point of intersection.

Complete step by step answer:
Using the graphing calculator:
On a TI graphing calculator,
Graph the first given equation i.e. y = x + 2.
Select TRACE
Input a value for x i.e. x = -3 (it is given in the question).
You will get y = -1.
Thus, it is the intersection point
Therefore, (-3, -1) is the intersection point.
We have given that,
$\Rightarrow y=x+2$ ------ (1) And
$\Rightarrow x=-3$ ------- (2)
As we know that the graph of the equation x = -3 will be a vertical line. This means for any value of ‘y’, the value of ‘x’ remains -3.
Now, solving the equation (1)
$\Rightarrow y=x+2$
Find the value of ‘x’ and ‘y’, we get
When y = 1, then
$\Rightarrow y=x+2$
$\Rightarrow 1=x+2$
$\Rightarrow x=-1$
When y = 3, then
$\Rightarrow 3=x+2$
$\Rightarrow x=1$
Therefore,

$x$	-1	1
$y$	1	3

Now, draw the graph of the equation,

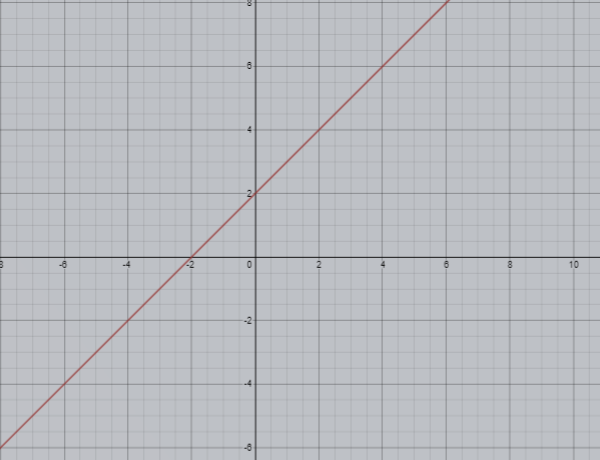
Now, solving the equation (2)
$\Rightarrow x=-3$
The graph of the equation x = -3 will be vertical line. This means for any value of ‘y’, the value of ‘x’ remain -3.
Thus, the graph of this equation,

Combining both the graphs, we get

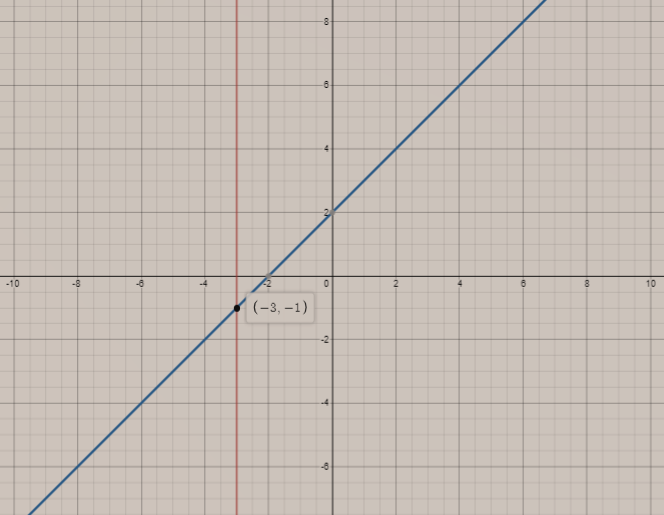
Therefore, we get the intersection point i.e. (-3 -1).

Note: You can use TI-84 plus graphing calculator to find the intersection point of two given equations. Using the trace option you will only get an approximation of intersection point as it rarely locates the accurate intersection point. It is easy to find the intersection point of two equations using the graphing calculator, students just need to remember the steps.