Solveeit Logo
Login

Question

Question: How do you find \[\theta \] if \[0 < \theta < 360\] and \[\cot \theta =-1\] and theta is in quadrant...

How do you find θ\theta if 0<θ<3600 < \theta < 360 and cot⁡θ=−1\cot \theta =-1 and theta is in quadrant IV?

Explanation

Solution

We are asked to find the value at an angle θ\theta such that cot⁡θ=−1\cot \theta =-1 and the angle lies in the fourth quadrant also with 0 to 360 degrees. To answer this we need to know first that when it is negative and then using that value, we will find when will it be negative in the fourth quadrant. As we know the fourth quadrant is 0 to 360 degrees, then the angle can range from 270 degrees to 360 degrees. So, our angle lies between them.

Complete step by step answer:
We are given that cot⁡θ\cot \theta is – 1 in the fourth quadrant. We have to find θ\theta such that it must be between 0 to 360 degrees. To answer this we will first see that when is cot⁡θ\cot \theta 1 in quadrant I and then we will use the property that cot⁡(−θ)=−cot⁡θ.\cot \left( -\theta \right)=-\cot \theta . To find −θ-\theta then we will convert this −θ-\theta angle into the angle that will lie in the fourth quadrant. Now, we know cot⁡θ\cot \theta is also defined at cot tangent. Both cot and tan ratio are 1 at the angle of 45 degrees. So, cot⁡45∘=1.\cot {{45}^{\circ }}=1. Hence, we get θ=45∘\theta ={{45}^{\circ }} in quadrant I where cot⁡θ\cot \theta is 1. We know cot⁡(−θ)=−cot⁡θ.\cot \left( -\theta \right)=-\cot \theta . So, as cot⁡(45∘)=1,\cot \left( {{45}^{\circ }} \right)=1, so we get,
cot⁡(−45∘)=−cot⁡(45∘)=−1\cot \left( -{{45}^{\circ }} \right)=-\cot \left( {{45}^{\circ }} \right)=-1
Hence,
cot⁡(−45∘)=−1\cot \left( -{{45}^{\circ }} \right)=-1
This means at θ=−45∘\theta =-{{45}^{\circ }} cot⁡θ\cot \theta is 45 degrees.
Now, −θ-\theta means that we moved θ\theta angle in the clockwise direction. So to find the actual angle, we will first learn using the graph.

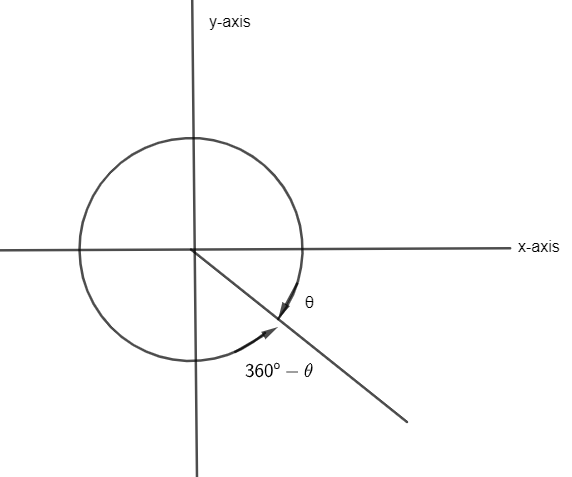
So, moving −θ∘-{{\theta }^{\circ }} in clockwise direction means going 360 degrees in anticlockwise direction. Hence, our angle will be 360∘−θ{{360}^{\circ }}-\theta that is 360∘−45∘.{{360}^{\circ }}-{{45}^{\circ }}. So, solving this we get, 360∘−45∘=315∘.{{360}^{\circ }}-{{45}^{\circ }}={{315}^{\circ }}.

Note: While finding angle in any quadrant we always find the angle in the first quadrant then we will use the following relation. If angle in quadrant I is θ\theta then angle in quadrant II is given as π−θ\pi -\theta or 180∘−θ.{{180}^{\circ }}-\theta . Angle in quadrant III is given as π+θ\pi +\theta or 180∘+θ{{180}^{\circ }}+\theta and lastly as done above, angle in quadrant IV is given as 2π−θ2\pi -\theta or 360∘−θ.{{360}^{\circ }}-\theta .