Question

How do you find the x and y intercepts of the given line $x-3y=-6$?

Answer 1

We start solving the problem by finding the intercept of the line with x-axis using the fact that the value of y coordinate is 0 on the x-axis. We then find the intercept of the line with y-axis using the fact that the value of x coordinate is 0 on the y-axis to get the required answer for the given problem.

Complete step by step solution:
According to the problem, we are asked to find the x and y intercepts of the given line $x-3y=-6$.
We can see that the given equation $x-3y=-6$ resembles the equation of line $ax+by+c=0$.
Let us find the intercept of the line with x-axis. We know that the value of y coordinate is 0 on the x-axis. Let us substitute $y=0$ in the line $x-3y=-6$.

$\Rightarrow x-3\left( 0 \right)=-6$.
$\Rightarrow x-0=-6$.
$\Rightarrow x=-6$.
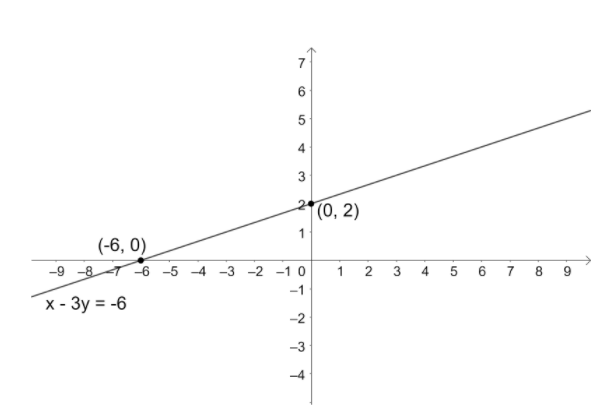
So, the x-intercept of the given line $x-3y=-6$ is –6.
Now, let us find the intercept of the line with y-axis. We know that the value of x coordinate is 0 on the y-axis. Let us substitute $x=0$ in the line $x-3y=-6$.
$\Rightarrow \left( 0 \right)-3y=-6$.
$\Rightarrow -3y=-6$.
$\Rightarrow y=\dfrac{-6}{-3}$.
$\Rightarrow y=2$.
So, the y-intercept of the given line $x-3y=-6$ is 2.
$\therefore$ we have found the x and y-intercepts of the given line $x-3y=-6$ as –6 and 2.

Note: We can also solve this problem by making use of the fact that the intercept of the line is defined as $\dfrac{x}{a}+\dfrac{y}{b}=1$, where x-intercept of the line is a and y-intercept of the line is b. We should not make calculation mistakes while solving this type of problem. Similarly, we can expect problems to find the point of intersection of the line $5x-2y=40$ with both axes.