Question

How do you find the $x$ and $y$ intercepts for $y = 2{x^2} + 8x + 10$?

Answer 1

The $x$ intercepts for a curve on the graph are the points at which the curve intersects the x-axis. At these points $y = 0$. Similarly, $y$ intercepts for a curve on the graph are the points at which the curve intersects the y-axis. At these points $x = 0$.

Complete step by step solution:
We have to find $x$ and $y$ intercepts for the equation $y = 2{x^2} + 8x + 10$.
First we find the $x$ intercept.
The $x$ intercepts are the points at which the curve intersects the x-axis. To find the abscissa, i.e. $x$ coordinate, we assume $y = 0$ and evaluate the corresponding value of $x$.
$y = 2{x^2} + 8x + 10 \\\ \Rightarrow 0 = 2{x^2} + 8x + 10 \\\$
We have to solve the above quadratic equation to find the values of $x$.
The discriminant $D = {b^2} - 4ac$ of the equation is $D = {8^2} - 4 \times 2 \times 10 = 64 - 80 = - 16$. We see that the discriminant $D < 0$, so there are no real roots of this equation, i.e. no real values of $x$ satisfies the equation.
This means that the curve does not cut the x-axis for any real value of $x$.
Thus there are no $x$ intercepts of the graph of the given equation.
Now we try to find the $y$ intercept.
The $y$ intercepts are the points at which the curve intersects the y-axis. To find the ordinate, i.e. $y$ coordinate, we assume $x = 0$ and evaluate the corresponding value of $y$.
$y = 2{x^2} + 8x + 10 \\\ \Rightarrow y = 2 \times {0^2} + 8 \times 0 + 10 \\\ \Rightarrow y = 0 + 10 \\\ \Rightarrow y = 10 \\\$
Thus, we get the point as $(0,\,{\kern 1pt} {\kern 1pt} 10)$. This is the $y$ intercept of the graph of the given equation.
Hence, for the graph of the given equation we don’t have any $x$ intercept and the $y$ intercept is $(0,\,{\kern 1pt} {\kern 1pt} 10)$.
This we can also show from the graph of the equation $y = 2{x^2} + 8x + 10$.

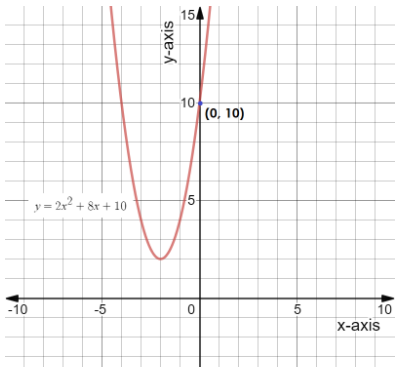
We can see in the above graph that the curve of the equation forms a parabola and cuts the y-axis at $(0,\,{\kern 1pt} {\kern 1pt} 10)$, whereas the curve is not cutting the x-axis at any point.

Note:
To find the $x$ intercept we put $y = 0$ and to find $y$ intercept we put $x = 0$ in the given equation. In case we don’t get any real values with this, it means that the curve is not cutting that axis at any point. In case of the parabola, then we get either zero or two intercepts at one axis and exactly one intercept at the other axis.