Question

How do you find the $x$ and $y$ intercepts for $y = 2x + 18$?

Answer 1

The $x$ intercepts for a curve on the graph are the points at which the curve intersects the x-axis. At these points $y = 0$. Similarly, $y$ intercepts for a curve on the graph are the points at which the curve intersects the y-axis. At these points $x = 0$.

Complete step by step solution:
We have to find $x$ and $y$ intercepts for the equation $y = 2x + 18$.
First we find the $x$ intercept.
The $x$ intercepts are the points at which the curve intersects the x-axis. To find the abscissa, i.e. $x$ coordinate, we assume $y = 0$ and evaluate the corresponding value of $x$.
$y = 2x + 18 \\\ \Rightarrow 0 = 2x + 18 \\\ \Rightarrow - 18 = 2x \\\ \Rightarrow \dfrac{{ - 18}}{2} = x \\\ \Rightarrow x = - 9 \\\$
Thus, we get the point as $( - 9,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0)$. This is the $x$ intercept of the graph of the given equation.
Now we find the $y$ intercept.
The $y$ intercepts are the points at which the curve intersects the y-axis. To find the ordinate, i.e. $y$ coordinate, we assume $x = 0$ and evaluate the corresponding value of $y$.
$y = 2x + 18 \\\ \Rightarrow y = 2 \times 0 + 18 \\\ \Rightarrow y = 0 + 18 \\\ \Rightarrow y = 18 \\\$
Thus, we get the point as $(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} 18)$. This is the $y$ intercept of the graph of the given equation.
Hence, for the graph of the given equation we get the $x$ intercept as $( - 9,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0)$ and the $y$ intercept as $(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} 18)$.
This we can also show from the graph of the equation $y = 2x + 18$.

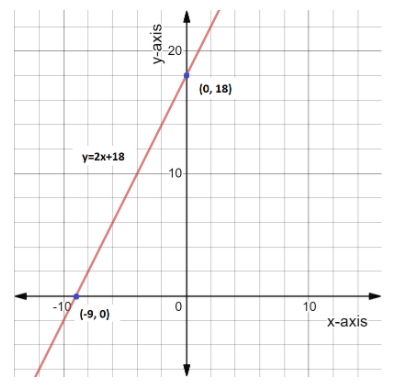
We can see in the above graph that the line of the equation cuts the x-axis at $( - 9,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0)$ and the y-axis at $(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} 18)$.

Note:
To find the $x$ intercept we put $y = 0$ and to find $y$ intercept we put $x = 0$ in the given equation. For a linear equation, we can also find the intercepts by writing the equation in the form of $\dfrac{x}{a} + \dfrac{y}{b} = 1$, where $a$ will be the $x$ intercept and $b$ will be the $y$ intercept. For a linear equation in two variables we get at most one $x$ intercept and at most one $y$ intercept.