Question

How do you find the $x$ and $y$ intercepts for $y=2{{x}^{3}}+3x-5$?

Answer 1

$x$ and $y$ intercepts for the given expression can be found by keeping one of the variables as zero. That is, to find the x intercept, the point at which the equation intersects the x-axis, we will have to keep $y=0$ and to find the y intercept, the point at which the equation intersects the y-axis, we will have to keep the $x=0$.

Complete step-by-step solution:
x- intercept refers to the point in the graph of a given equation which intersects the x-axis. At that point, y-coordinate will be zero. This information is important to find the x-intercept else we will have to draw the graph of the given equation.
Similarly, y- intercept refers to the point in the graph of a given equation which intersects the y-axis. At that point, x coordinate will be zero. This information is important to find the y-intercept else we will have to draw the graph of the given equation. We will verify our answer with the help of a graph at the end.
According to the given question, we are to find the $x$ and $y$ intercepts for $y=2{{x}^{3}}+3x-5$,
Let’s start with finding x-intercept,
We will take $y=0$
So the equation gets the form,
$2{{x}^{3}}+3x-5=0$
Now solving the equation for the value of $x$, since the degree of the polynomial is 3, we will get three values of $x$.
$\Rightarrow 2{{x}^{3}}+3x=5$
Taking $x$ common, we get
$\Rightarrow x(2{{x}^{2}}+3)=5$
We have $x=5$ and $2{{x}^{2}}+3=5$
So, one value of $x=5$, since it does not satisfy the equation it is removed, solving other part,
$2{{x}^{2}}+3=5$
$\Rightarrow 2{{x}^{2}}=2$
$\Rightarrow {{x}^{2}}=1$
$x=\pm 1$
Since, $x=-1$does not satisfy the equation it is removed as well.
Now, we only have $x=1$
So, we get the value of x-intercept in the equation: $(1,0)$
Now, let’s find the y-intercept,
We will take $x=0$, we get the equation as
$y=2(0)+3(0)-5$
$y=-5$
So, the y-intercept is $(0,-5)$.

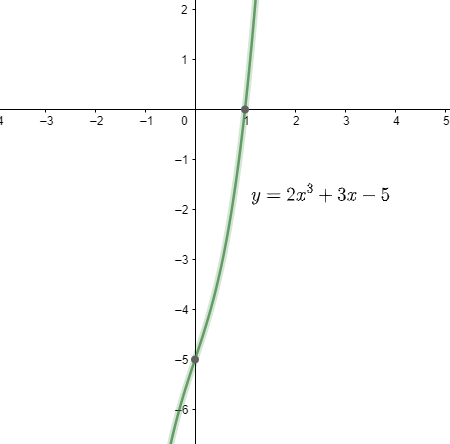
Therefore, the $x$ and $y$ intercepts for $y=2{{x}^{3}}+3x-5$ are:
x-intercept in the equation is $(1,0)$
y-intercept is $(0,-5)$

Note: $x$ and $y$ intercept are found by taking $y=0$ and $x=0$ respectively. It should be kept in mind while doing the calculation and not interpreted the other way round. Also while substituting the values of $x$ and $y$, it should be calculated carefully else will result in a wrong answer.