Question

How do you find the x and y-intercept for $y=-2x+4$?

Answer 1

The above given question is a linear equation in one variable. Since, we know that the slope intercept form of the line equation is given as y = mx + c, where m is the slope of the line and c is the y-intercept. In the given equation $y=-2x+4$, we have m = -2 and $c=4$ . So, we will say that the line $y=6x+4$ has slope equal to 6 and y-intercept equal to 4 and to find x-intercept of $y=-2x+4$we will put y = 0 in the above equation and find value of x which is the x-intercept of the given equation.

Complete step-by-step solution:
We know that the above question is a linear equation in one variable.
We also know that the slope-intercept form of the linear equation is given y = mx + c, where m is the slope of the line and c is the y-intercept. Slope is the tangent of the angle made by the line with x-axis and y-intercept is the point at which the line cuts the y-axis and x-intercept is the point at which the line cuts the x-axis
Now, we will compare the equation $y=-2x+4$ with the general equation y = mx + c.
After comparing we will get: m = -2 and $c=4$.
So, the slope of the line $y=-2x+4$ is equal to -2, and the y-intercept is equal to 4 .
Now, we will find the x-intercept of the line by putting y = 0 in the above equation $y=-2x+4$.
So, we will get:
$\begin{aligned} & \Rightarrow 0 =-2\left( x \right)+4 \\\ & \Rightarrow x = 2 \\\ \end{aligned}$
Hence, line $y=-2x+4$ intersect the x-axis at the point (2, 0).
Hence, x-intercept of line $y=-2x+4$ is equal to 2.
We can plot the graph of the line $y=-2x+4$ as:

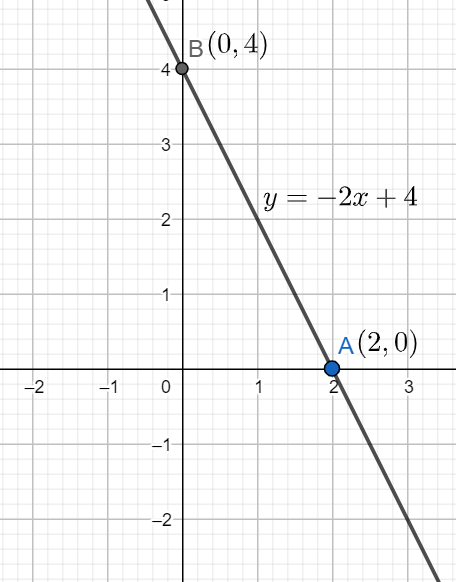
This is our required solution.

Note: Student are required to note that when we have general equation of the line as $ax+by+c=0$, then slope of the line is equal to $-\dfrac{a}{b}$ and y-intercept is equal to $-\dfrac{c}{a}$. We can also find the slope of the line by equating the first derivative of the line equation to 0 i.e. $\dfrac{dy}{dx}=0$ and when we put x = 0, we will get the y-intercept of the line.