Question

How do you find the volume of the solid generated by revolving the region bounded by $y={{x}^{2}},y=0,x=2$
(i) about the X-axis
(ii) about the Y-axis

Answer 1

We first find the area region bounded by the curves and lines $y={{x}^{2}},y=0,x=2$. Then we use the rotation and the volume formulas to find the integration and the solution of the problem.

Complete step by step solution:
We have to find the volume of the solid generated by revolving the region bounded by $y={{x}^{2}},y=0,x=2$
Then we need to do it revolving twice, once about the X-axis and then about the Y-axis.
We first try to find the area bounded by the region bounded by $y={{x}^{2}},y=0,x=2$.

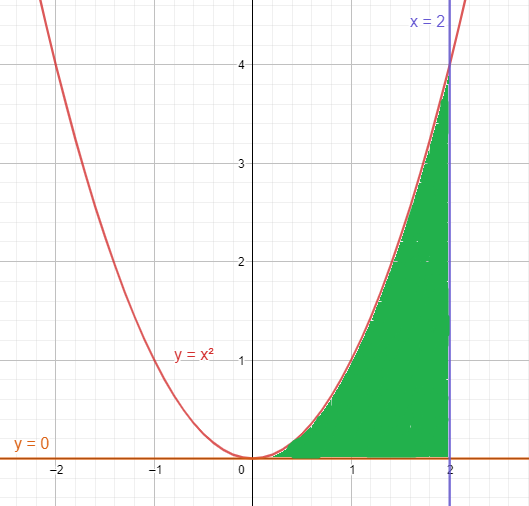
The shaded area is the bounded area which will be rotated.
We first rotate it about the X-axis.
The region will be covering the whole area in a circle-based form where we have to find the volume with respect the y intersects.
To get a solid of revolution we start out with a function, $y=f\left( x \right)f\left( x \right)$, on an interval $\left[ a,b \right]$. We then rotate this curve about a given axis to get the surface of the solid of revolution.
Therefore, we are trying to form the integration for the volume along the y intersects.
The lines $y=0,x=2$ gives the boundary.
We now integrate $y={{x}^{2}}$ with the volume formula where $V=\pi \int\limits_{a}^{b}{{{y}^{2}}dx}$.
Putting the values, we get $V=\pi \int\limits_{0}^{2}{{{y}^{2}}dx}$. We have the equation $y={{x}^{2}}$.
So, $V=\pi \int\limits_{0}^{2}{{{x}^{4}}dx}=\pi \left[ \dfrac{{{x}^{5}}}{5} \right]_{0}^{2}$. Putting the values, we get $V=\pi \left[ \dfrac{{{x}^{5}}}{5} \right]_{0}^{2}=\dfrac{32\pi }{5}$ cubic unit.
Now for rotation about Y-axis, we integrate $x=\sqrt{y}$ with the volume formula where $V=\pi \int\limits_{a}^{b}{\left[ {{x}_{2}}^{2}-{{x}_{1}}^{2} \right]dx}$.
So, $V=\pi \int\limits_{0}^{4}{\left[ {{2}^{2}}-y \right]dy}=\pi \left[ 4y-\dfrac{{{y}^{2}}}{2} \right]_{0}^{4}=\pi \left[ 16-8 \right]=8\pi$ cubic unit.
Therefore, the volumes are $\dfrac{32\pi }{5},8\pi$ cubic units respectively.

Note: Consider the same function with $f\left( x \right)=1$. When rotated, it will look similar to our previous rotation but with a cylinder removed in the middle. To find the volume, we simply take the difference of our original area and the area of the space in the centre.