Question

How do you find the volume of the region below $y=-3x+6$ and enclosed by the $y$-axis from $0$ to $2$, rotated about the $x$-axis?

Answer 1

In this question we have to find the volume of a region which is enclosed by the given points. We will first write the region in terms of all the limitations of the region and then plot them on the graph to get the points of the shape. We will then split the plane into two shapes and find the volume for both the shapes and add them to get the final volume.

Complete step-by-step solution:
We know that the region lies below $y= -3x+6$, is enclosed by the $y$-axis from $0$ to $2$ therefore, we can write:
$y\ge 0$
$y\le 0$
$y\le -3x+6$
$x\ge 0$
On drawing the figure on the graph, we get:

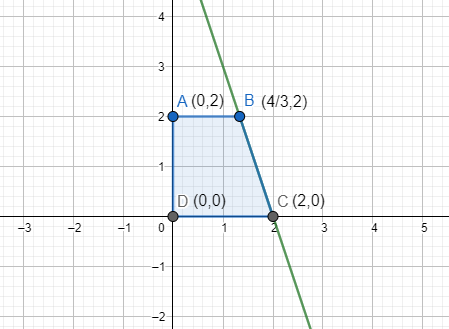
Now the formula for calculating the volume of the solid from revolution around the $x$-axis is:
$V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}$
But we have a composite function since the plane has variable values of $y$ when $x$ changes therefore, we can write our function as:
f\left( x \right)=\left\\{ \begin{matrix} y=2 & \text{if 0}\le \text{x}\le \dfrac{4}{3} \\\ y=-3x+6 & \text{if }\dfrac{4}{3}\le \text{x}\le 2 \\\ \end{matrix} \right.
Therefore, we will break our solid into two shapes, a cylinder from $x=0$ to $x=\dfrac{4}{3}$ and a cone from $x=\dfrac{4}{3}$ to $x=2$.
We have the total volume as:
${{V}_{tot}}={{V}_{cylinder}}+{{V}_{cone}}$
Now we have the volume of the cylinder as:
$\Rightarrow {{V}_{cylinder}}=\pi \int\limits_{0}^{\dfrac{4}{3}}{{{f}^{2}}\left( x \right)dx}$
On substituting the value of $f\left( x \right)=2$, we get:
$\Rightarrow {{V}_{cylinder}}=\pi \int\limits_{0}^{\dfrac{4}{3}}{{{2}^{2}}dx}$
On simplifying, we get:
$\Rightarrow {{V}_{cylinder}}=\pi \int\limits_{0}^{\dfrac{4}{3}}{4dx}$
Now we know $\int{k}dx=kx+c$ therefore, we get:
$\Rightarrow {{V}_{cylinder}}=\pi \left[ 4x \right]_{0}^{\dfrac{4}{3}}$
On substituting the values, we get:
$\Rightarrow {{V}_{cylinder}}=\pi \left( 4\left( \dfrac{4}{3} \right)-4\left( 0 \right) \right)$
On simplifying, we get:
$\Rightarrow {{V}_{cylinder}}=\dfrac{16\pi }{3}$
Now we have the volume of the cone as:
$\Rightarrow {{V}_{cone}}=\pi \int\limits_{0}^{\dfrac{4}{3}}{{{\left( -3x+6 \right)}^{2}}dx}$
On expanding the terms, we get:
$\Rightarrow {{V}_{cone}}=\pi \int\limits_{0}^{\dfrac{4}{3}}{\left( 9{{x}^{2}}-36x+36 \right)dx}$
Now we know that $\int{{{x}^{n}}}=\dfrac{{{x}^{n+1}}}{n+1}+c$therefore, we get:
$\Rightarrow {{V}_{cone}}=\pi \left[ 3{{x}^{3}}-18{{x}^{2}}+36x \right]_{\dfrac{4}{3}}^{2}$
On substituting the values, we get:
$\Rightarrow {{V}_{cone}}=\pi \left( 3\times {{2}^{3}}-18\times {{2}^{2}}+36\times 2-3{{\left( \dfrac{4}{3} \right)}^{3}}+18{{\left( \dfrac{4}{3} \right)}^{2}}-36\left( \dfrac{4}{3} \right) \right)$
On simplifying, we get:
$\Rightarrow {{V}_{cone}}=\pi \left( 24-72+72-\dfrac{64}{9}+\dfrac{288}{9}-48 \right)$
On further simplification, we get:
$\Rightarrow {{V}_{cone}}=\pi \left( -\dfrac{216}{9}-\dfrac{64}{9}+\dfrac{288}{9} \right)$
On adding all the fractions, we get:
$\Rightarrow {{V}_{cone}}=\dfrac{8\pi }{9}$
Therefore, the total volume will be:
${{V}_{tot}}={{V}_{cylinder}}+{{V}_{cone}}$
On substituting the values, we get:
${{V}_{tot}}=\dfrac{16\pi }{3}+\dfrac{8\pi }{9}$
On simplifying, we get:
${{V}_{tot}}=\dfrac{56\pi }{9}$, which is the required solution.

Note: In this question we have used integral calculus to find the volume of the given solid. We used the concept of definite integrals where integration is done on a specific figure also called as a plane between two limits. There also exists indefinite integrals which do not have any limiting value. Definite integrals are used to find the area and volumes of planes and solids respectively.