Question

How do you find the volume bounded by $y=\ln \left( x \right)$ and the lines y = 0, x = 2 and revolve about the y – axis?

Answer 1

Convert the logarithmic function into the exponential function by using the formula if $y=\ln \left( x \right)$ then $x={{e}^{y}}$. Assume x = 2 as f (y) and $x={{e}^{y}}$ as g (y). Use the formula: $V=\int_{a}^{b}{\pi \left[ {{\left[ f\left( y \right) \right]}^{2}}-{{\left[ g\left( y \right) \right]}^{2}} \right]dy}$ to find the volume of revolution of a curve about the y axis. Here V is the volume, ’a’ and ‘b’ are the lower and upper limits respectively. Here, a will be y = 0 and b will be the value of y for which x = 2. Find the integral and substitute the limits to get the answer.

Complete step by step answer:
Here we have been provided with the curve $y=\ln \left( x \right)$ and the lines y = 0, x = 2. We are asked to determine the volume of revolution of the bounded part about the y axis.
In general, the volume bounded by the two curves ${{x}_{1}}=f\left( y \right)$ and ${{x}_{2}}=g\left( y \right)$ revolved about the y – axis is given by the formula: $V=\int_{a}^{b}{\pi \left[ {{\left[ f\left( y \right) \right]}^{2}}-{{\left[ g\left( y \right) \right]}^{2}} \right]dy}$, where V is the volume, ’a’ and ‘b’ are the lower and upper limits respectively.

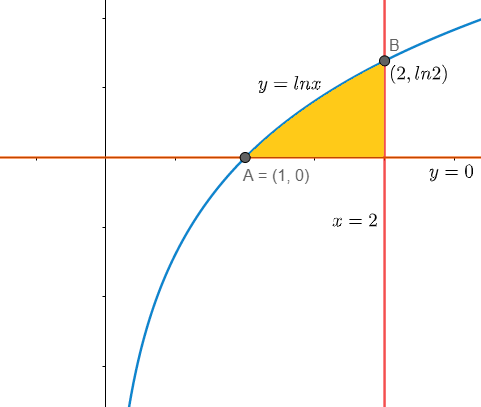
So, first we need to determine x as function of y. Here we have $y=\ln \left( x \right)$, therefore changing it into the exponential function we get $x={{e}^{y}}$. From the above graph it is clear that we have to assume $f\left( y \right)=2$ and $g\left( y \right)={{e}^{y}}$ to get the volume positive. Now, the lower limit is a = 0 and the upper limit will be the value of y for which the value of is 2, i.e. $b=\ln 2$. Substituting all the values in the formula we get,

& \Rightarrow V=\int_{0}^{\ln 2}{\pi \left[ {{\left[ 2 \right]}^{2}}-{{\left[ {{e}^{y}} \right]}^{2}} \right]dy} \\\ & \Rightarrow V=\pi \int_{0}^{\ln 2}{\left[ 4-{{e}^{2y}} \right]dy} \\\ & \Rightarrow V=\pi \left[ 4y-\dfrac{{{e}^{2y}}}{2} \right]_{0}^{\ln 2} \\\ \end{aligned}$$ Substituting the limits we get, $$\begin{aligned} & \Rightarrow V=\pi \left[ \left( 4\left( \ln 2 \right)-\dfrac{{{e}^{2\ln 2}}}{2} \right)-\left( 4\left( 0 \right)-\dfrac{{{e}^{2\left( 0 \right)}}}{2} \right) \right] \\\ & \Rightarrow V=\pi \left[ \left( 4\ln 2-\dfrac{{{e}^{2\ln 2}}}{2} \right)+\dfrac{1}{2} \right] \\\ \end{aligned}$$ Using the formula $m\log a=\log {{a}^{m}}$ and ${{a}^{{{\log }_{a}}b}}=b$ we get, $$\begin{aligned} & \Rightarrow V=\pi \left[ \left( 4\ln 2-\dfrac{4}{2} \right)+\dfrac{1}{2} \right] \\\ & \therefore V=\pi \left( 4\ln 2-\dfrac{3}{2} \right) \\\ \end{aligned}$$ **Hence, the volume of revolution is $$\pi \left( 4\ln 2-\dfrac{3}{2} \right)$$ cubic units.** **Note:** You must remember the formula of volume of revolution both about the y and x axis. In case the curve is revolved around the x – axis the formula becomes $$V=\int_{a}^{b}{\pi \left[ {{\left[ f\left( x \right) \right]}^{2}}-{{\left[ g\left( x \right) \right]}^{2}} \right]dx}$$ and the values of ‘a’ and ‘b’ will be the limits of x. You must be careful while finding the limits. Do not forget to draw the graph for better understanding.