Question

How do you find the vertex, $x$ - intercept, $y$ - intercept, and graph the equation $y = - 4{x^2} + 20x - 24$?

Answer 1

This question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. We need to know the basic formula to find vertex from the given equation. Also, we need to know the basic conditions for finding$x$-intercept and $y$ -intercept. We need to know how to draw a graph with the given equation. Also, we need to know the basic form of a quadratic equation.

Complete step by step solution:
The given equation is shown below,
$y = - 4{x^2} + 20x - 24 \to \left( 1 \right)$
The basic form of a quadratic equation is,
$y = a{x^2} + bx + c$
So, the value of

$$a = - 4 \\\ b = 20 \\\ c = - 24 \\\$$

We know that if the value $a$ is negative, then the parabolic shape will be in a downward position.
The basic form of the vertex is $\left( {h,k} \right)$. Let’s find the value of $h$,
We know that,
$h = \dfrac{{ - b}}{{2a}} \to \left( 2 \right)$
By substituting the values of$a = - 4$and$b = 20$in the above equation we get,

$$h = \dfrac{{ - 20}}{{2 \times - 4}} = \dfrac{{ - 20}}{{ - 8}} \\\ h = \dfrac{5}{2} \\\$$

For finding the value of $k$, we substitute the value of $h$in the equation $\left( 1 \right)$instead of$x$. So, we get
$\left( 1 \right) \to y = - 4{x^2} + 20x - 24$

$$y = - 4{\left( {\dfrac{5}{2}} \right)^2} + 20\left( {\dfrac{5}{2}} \right) - 24 \\\ y = - 4\left( {\dfrac{{25}}{4}} \right) + \left( {10 \times 5} \right) - 24 \\\ y = - 25 + 50 - 24 \\\$$

$y = 1$
Take$y$as$k$
So, we get $\left( {h,k} \right) = \left( {\dfrac{5}{2},1} \right)$
The vertex point is $\left( {h,k} \right) = \left( {\dfrac{5}{2},1} \right)$
Next, we would find $x$ and $y$ -intercept. We know that if we want to find $x$ -intercept, then we have to set $y$ is equal to zero. If we want to find $y$ -intercept, then we have to set $x$ is equal to
zero.
Set $y = 0$in the equation$\left( 1 \right)$, we get
$\left( 1 \right) \to y = - 4{x^2} + 20x - 24$
$0 = - 4{x^2} + 20x - 24$
Divide$- 4$into both sides
$0 = {x^2} - 5x + 24$
By factoring the above equation we get,

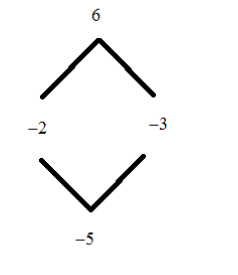
So, we get
$\left( {x - 2} \right)\left( {x - 3} \right) = 0$
So, we get$x = 3,x = 2$when$y = 0$
Next set$x = 0$in the equation$\left( 1 \right)$, we get
$\left( 1 \right) \to y = - 4{x^2} + 20x - 24$

$$y = - 4{\left( 0 \right)^2} + (20 \times 0) - 24 \\\ y = 0 + 0 - 24 \\\$$

$y = - 24$
So, we get$y = - 24$when$x = 0$
So, we have,
$y$-intercept$= \left( {0, - 24} \right)$
$x$-intercept$= \left( {3,0} \right),\left( {2,0} \right)$
Vertex$= \left( {\dfrac{5}{2},1} \right)or\left( {2.5,1} \right)$
Let’s plot these points in the graph sheet as shown below,

Note: Remember the formula and conditions for x -intercept, y -intercept, and vertex point. Note that if a is negative the parabola shape will be in a downward position and if a is positive the parabola shape will be in an upward position. Also, this question describes the operation of addition/ subtraction/ multiplication/ division.