Question

How do you find the vertex, the y-intercept, and symmetric point, and use these to sketch the graph given $y = 5{x^2} - 30x + 31$?

Answer 1

We have given an equation as $y = 5{x^2} - 30x + 31$ , which is a parabolic equation. The standard parabolic equation is always represented as $y = a{x^2} + bx + c$ and the expression $- \dfrac{b}{{2a}}$ gives the x-coordinate , and then substitute x-coordinate in the original equation to obtain y-coordinate.

Complete step by step answer:
We have given an equation of parabola $y = 5{x^2} - 30x + 31$, (original equation)
We have to find the vertex of parabola ,
We know that the standard parabolic equation is always represented as $y = a{x^2} + bx + c$ and the expression $- \dfrac{b}{{2a}}$ gives the x-coordinate , and when we substitute x-coordinate in the original equation we get the y-coordinate.
Now, compare the original equation with the standard parabolic equation, we will get,
The x-coordinate of the vertex , $- \dfrac{b}{{2a}} = - \dfrac{{( - 30)}}{{2(5)}}$ $= 3$
Now substitute $x = 3$ in the original equation to get y-coordinate as,
$\Rightarrow y = 5{x^2} - 30x + 31$
$\Rightarrow y = 5{(3)^2} - 30(3) + 31$
$= 45 - 90 + 31$
$= - 45 + 31$
$= - 14$
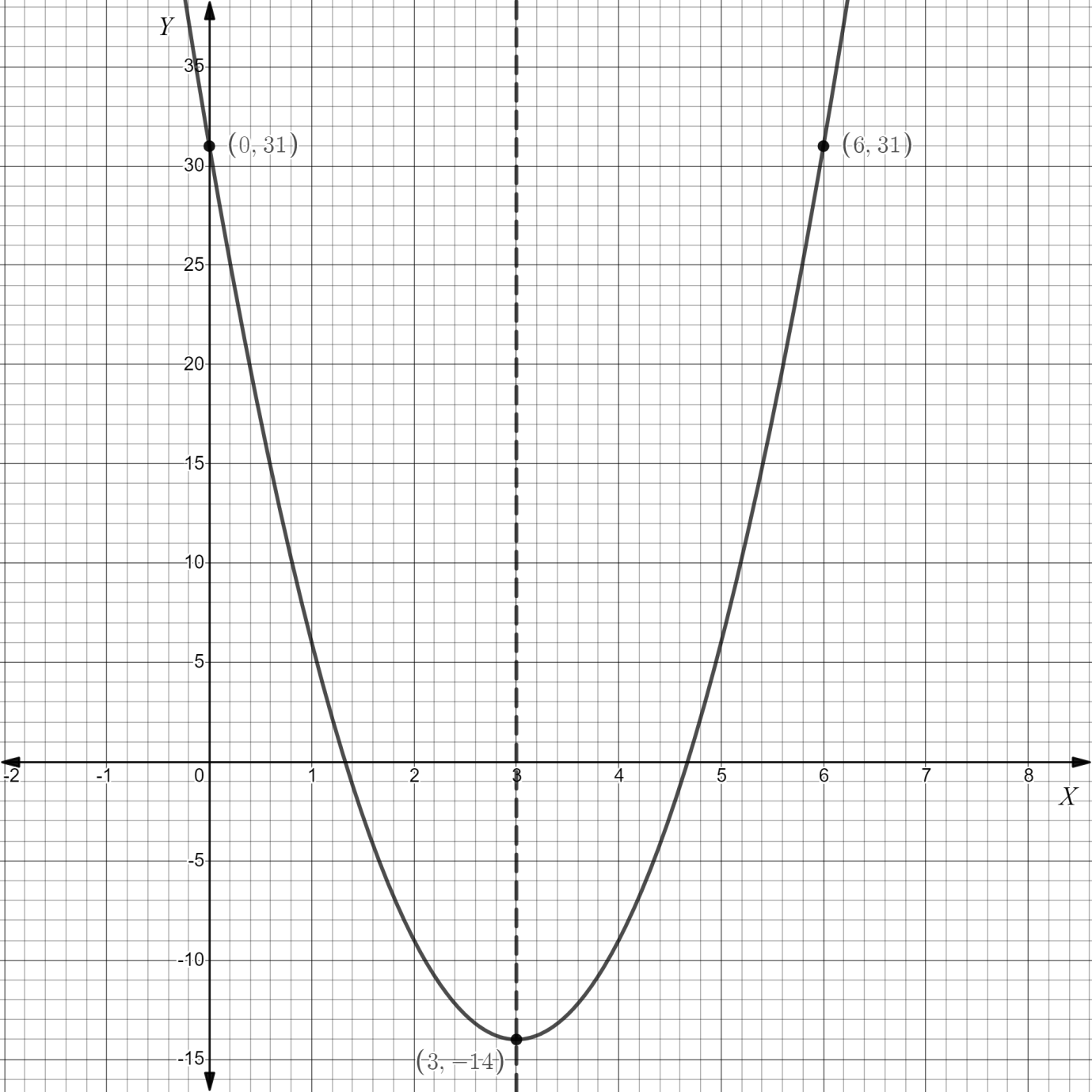
Therefore, the required vertex of the parabola is $\left( {3, - 14} \right)$ . For y-intercept put $x = 0$ ,
$\Rightarrow y = 5{x^2} - 30x + 31$
$= 5{(0)^2} - 30(0) + 31$
$= 31$
Therefore, we have $y = 31$ as a y-intercept.
As we know that parabola is always symmetric about its vertex. Therefore, we can consider vertex as a symmetric point.
Graphing Mark a point where the vertex is, then mark the point with the y-intercept, and use the concept of symmetry to draw a third point at $(6,31)$. Draw a dashed vertical line over the vertex and show that this line is a line of symmetry.
So the graph of the given equation will be as follows

Note: The equation for a parabola can also be written in vertex form as $y = a{(x - h)^2} + k$ where $(h,k)$ is the vertex of parabola. The point where a parabola has zero gradient is known as the vertex of the parabola. We need to get ‘y’ on one side of the “equals” sign, and all the other numbers on the other side.