Solveeit Logo
Login

Question

Question: How do you find the vertex of the parabola: \[y={{x}^{2}}+4x-5\]?...

How do you find the vertex of the parabola: y=x2+4x−5y={{x}^{2}}+4x-5?

Explanation

Solution

This question belongs to the topic of quadratic equation and their graphs. In this question, we are going to use a formula for finding the x coordinate of vertex of the parabola. For general equation of the parabolay=ax2+bx+cy=a{{x}^{2}}+bx+c , the x-coordinate of the vertex of the graph of parabola will be x=−b2ax=-\dfrac{b}{2a}. We can take reference from the following figure:

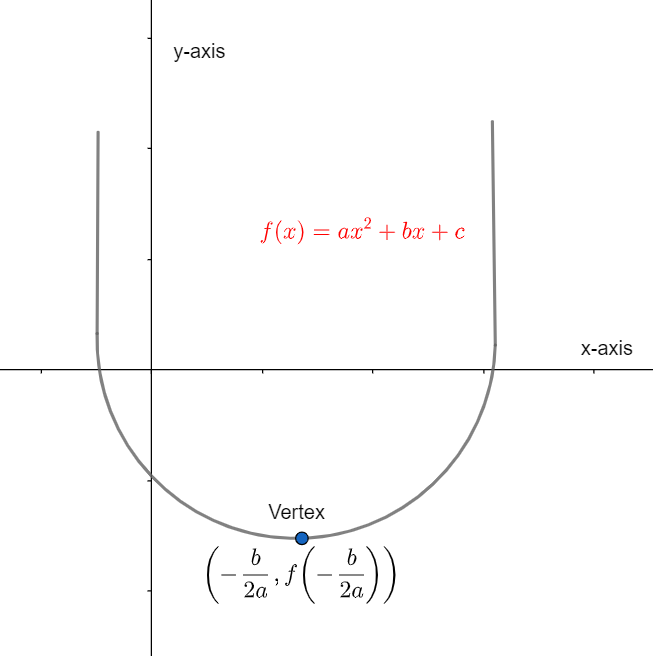
Complete step-by-step answer:
Let us solve this question.
In this question, we have to find the vertex of the parabola having the equationy=x2+4x−5y={{x}^{2}}+4x-5.
We going to use a formula for finding the point of vertex of parabola (let us suppose the point of vertex is (x,y))
The formula for finding the x-coordinate of the vertex of parabola is x=−b2ax=-\dfrac{b}{2a}, if the equation of parabola is y=ax2+bx+cy=a{{x}^{2}}+bx+c.
So, in this question, the equation is y=x2+4x−5y={{x}^{2}}+4x-5
Comparing the equation y=x2+4x−5y={{x}^{2}}+4x-5 with the equationy=ax2+bx+cy=a{{x}^{2}}+bx+c, we can say that
a=1, b=4, and c=-5
So, the x-coordinate of the vertex of parabola y=x2+4x−5y={{x}^{2}}+4x-5 will be
x=−b2a=−42×1=−2x=-\dfrac{b}{2a}=-\dfrac{4}{2\times 1}=-2
Hence, the x-coordinate of the vertex of parabola is -2.
Now, for the y-coordinate of the vertex of parabola, we will put the value of x as -2 in the equation of given parabola which is y=x2+4x−5y={{x}^{2}}+4x-5
Putting the value of x as -2 in the equationy=x2+4x−5y={{x}^{2}}+4x-5, we get
⇒y=(−2)2+4(−2)−5=4−8−5=−9\Rightarrow y={{\left( -2 \right)}^{2}}+4\left( -2 \right)-5=4-8-5=-9
So, the value of y is -9. Hence, we have got the y-coordinate of the vertex of parabola as -9.
Therefore, the vertex of parabola is (-2,-9).
We can take reference for the vertex from the following figure:

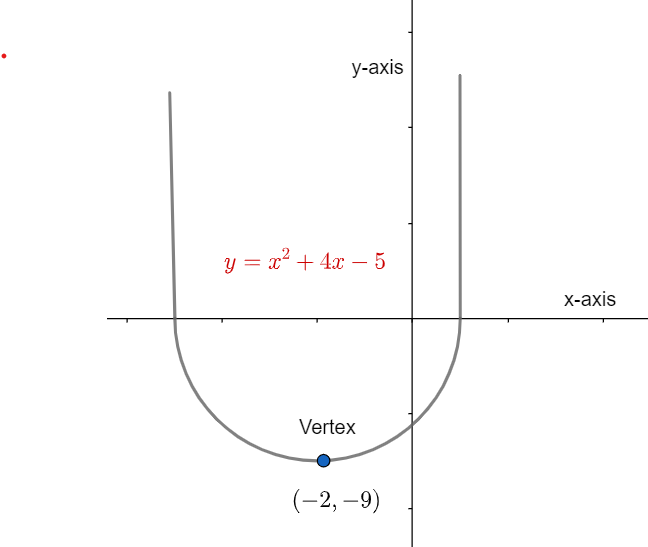
Note: We have an alternate method to solve this question.
The given equation is y=x2+4x−5y={{x}^{2}}+4x-5
Now, we will convert the right side of the equation as a perfect square.
The above equation can also be written as
⇒y+5=x2+4x\Rightarrow y+5={{x}^{2}}+4x
Now, adding 4 to both side of equation, we get
⇒y+5+4=x2+4x+4\Rightarrow y+5+4={{x}^{2}}+4x+4
Now, we can see that the right side of the equation is a perfect square of (x+2).
So, we can write the above equation as
⇒y+9=(x+2)2\Rightarrow y+9={{\left( x+2 \right)}^{2}}
If an equation of parabola is in the form ofy−k=a(x−h)2y-k=a{{\left( x-h \right)}^{2}}, then the vertex of parabola is (h,k).
⇒y−(−9)=(x−(−2))2\Rightarrow y-\left( -9 \right)={{\left( x-\left( -2 \right) \right)}^{2}}
So, we can say that the vertex of parabola will be (-2,-9)