Question

How do you find the vertex of the parabola: $y = {x^2} + 2x + 2$?

Answer 1

We have to find the vertex for $f\left( x \right) = {x^2} + 2x + 2$. First rewrite the equation in vertex form. Next, use the vertex form of parabola, to determine the values of $a$, $h$, and $k$. Next, find the vertex by putting the value of $h$ and $k$.
Vertex form of a parabola: $a{\left( {x + d} \right)^2} + e$
$d = \dfrac{b}{{2a}}$
$e = c - \dfrac{{{b^2}}}{{4a}}$
Vertex form: $y = a{\left( {x - h} \right)^2} + k$
Vertex: $\left( {h,k} \right)$
$p = \dfrac{1}{{4a}}$
Focus: $\left( {h,k + p} \right)$
Directrix: $y = k - p$

Complete step by step answer:
We have to find the vertex for $f\left( x \right) = {x^2} + 2x + 2$.
So, compare ${x^2} + 2x + 2$ with $a{x^2} + bx + c$.
So, first rewrite the equation in vertex form.
For this, complete the square for ${x^2} + 2x + 2$.
Use the form $a{x^2} + bx + c$, to find the values of $a$, $b$, and $c$.
$a = 1,b = 2,c = 2$
Consider the vertex form of a parabola.
$a{\left( {x + d} \right)^2} + e$
Now, substitute the values of $a$ and $b$ into the formula $d = \dfrac{b}{{2a}}$.
$d = \dfrac{2}{{2 \times 1}}$
Simplify the right side.
$\Rightarrow d = 1$
Find the value of $e$ using the formula $e = c - \dfrac{{{b^2}}}{{4a}}$.
$e = 2 - \dfrac{{{2^2}}}{{4 \times 1}}$
$\Rightarrow e = 1$
Now, substitute the values of $a$, $d$, and $e$ into the vertex form $a{\left( {x + d} \right)^2} + e$.
${\left( {x + 1} \right)^2} + 1$
Set $y$ equal to the new right side.
$y = {\left( {x + 1} \right)^2} + 1$
Now, use the vertex form, $y = a{\left( {x - h} \right)^2} + k$, to determine the values of $a$, $h$, and $k$.
$a = 1$
$h = 1$
$k = 1$
Since the value of $a$ is positive, the parabola opens up.
Opens Up
Find the vertex $\left( {h,k} \right)$.
$\left( { - 1,1} \right)$

Hence, the vertex of the parabola: $y = {x^2} + 2x + 2$ is at $\left( { - 1,1} \right)$.

Note: We can also determine the vertex of the parabola: $y = {x^2} + 2x + 2$ by plotting it.
Graph of $y = {x^2} + 2x + 2$:

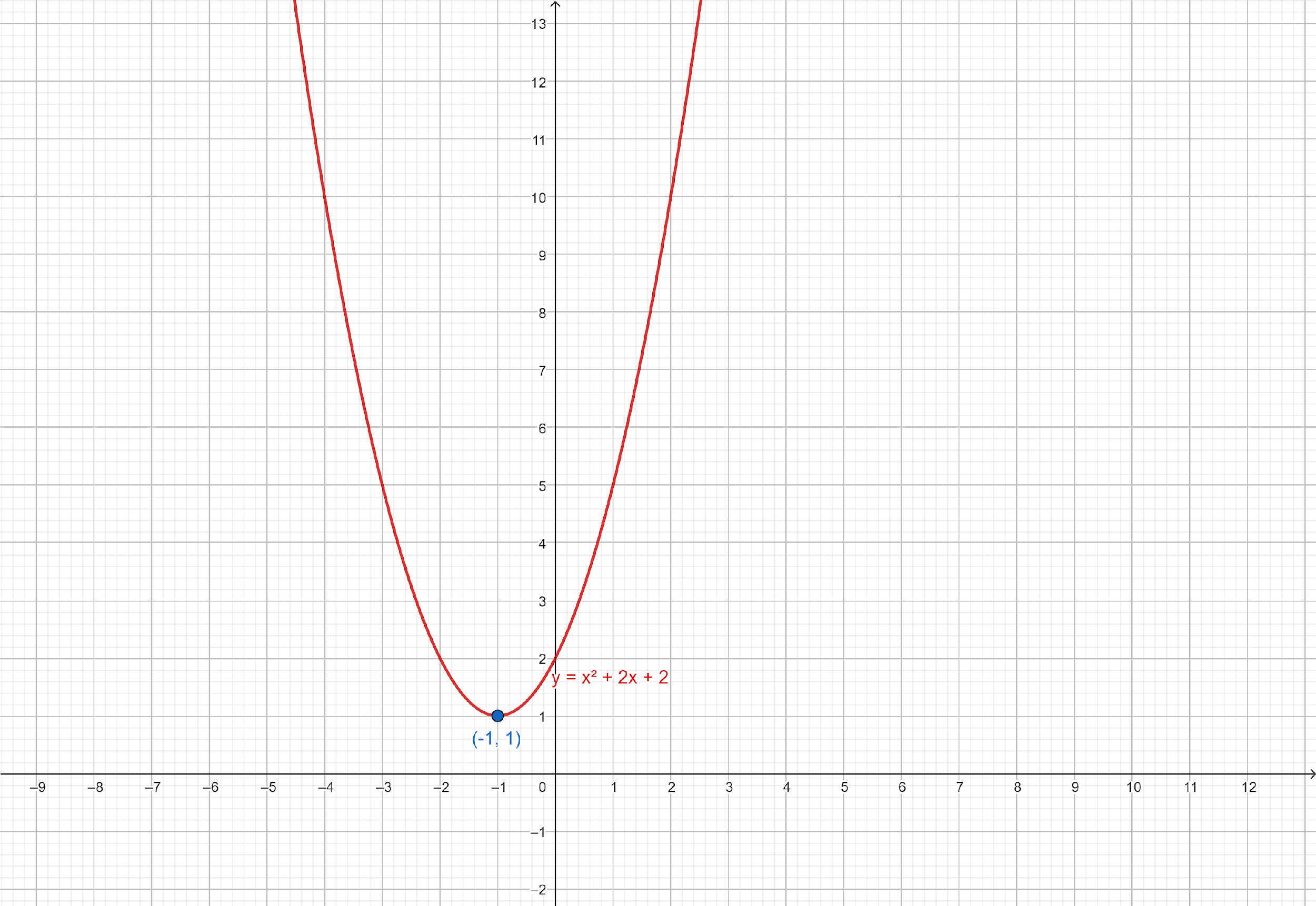
Hence, the vertex of the parabola: $y = {x^2} + 2x + 2$ is at $\left( { - 1,1} \right)$.
2. We can also determine the vertex of the parabola: $y = {x^2} + 2x + 2$ by converting to Vertex Form
Vertex form can be represented as $y = {\left( {x - h} \right)^2} + k$
where the point $\left( {h,k} \right)$ is the vertex.
To do that, we should complete the square
$y = {x^2} + 2x + 2$
First, we should try to change the last number in a way so we can factor the entire thing
⇒ we should aim for $y = {x^2} + 2x + 1$
to make it look like $y = {\left( {x + 1} \right)^2}$
If we notice, the only difference between the original $y = {x^2} + 2x + 2$ and the factor-able $y = {x^2} + 2x + 1$ is simply changing the 2 to a 1.
Since we can't randomly change the 2 to a 1, we can add 1 and subtract a 1 to the equation at the same time to keep it balanced.
So, we get
$y = {x^2} + 2x + 1 + 2 - 1$
Organizing
$y = \left( {{x^2} + 2x + 1} \right) + 2 - 1$
Add like terms
$2 - 1 = 1$
Factor
$y = {\left( {x + 1} \right)^2} + 1$
Now comparing it to $y = {\left( {x - h} \right)^2} + k$
We can see that the vertex would be $\left( { - 1,1} \right)$.