Question

How do you find the vertex of the parabola by completing the square ${x^2} - 6x + 8 = y$ ?

Answer 1

Hint : Here, the parabola is a U-shaped plane curve where any point is at an equal distance from a fixed point is focus, vertex. The given equation of parabola is needed to find the vertex $(h,k)$ of parabola.The vertex of a parabola is the point at the intersection of the parabola and its line of symmetry. For a parabola whose equation is given in standard form, the vertex will be the minimum (lowest point) of the graph and the maximum (highest point) of the graph.

Complete step by step solution:
We know that,
The vertex formula is $y = a{(x - h)^2} + k$ .
The equation of parabola, ${x^2} - 6x + 8 = y$
By rewrite equation, we get
$y = {x^2} - 6x + 9 - 1$
By simplify the above equation,
$y = ({x^2} - 2 \cdot 3x + {3^2}) - 1$
By write the equation by using the algebraic formula is ${(a + b)^2} = {a^2} + 2ab + {b^2}$ , we get
$y = {(x - 3)^2} - 1$ ………………. $(A)$
Use the vertex equation, $y = a{(x - h)^2} + k$ . To determine the value $a,h$ and $k$ , we get
From the equation $(A)$ , we get the value $a,h$ and $k$

$$a = 1 \\\ h = 3 \\\ k = - 1 \;$$

Therefore, the vertex of the parabola $(h,k)$ is $(3, - 1)$ .
To plot a graph with the vertex point and the parabola equation is given below

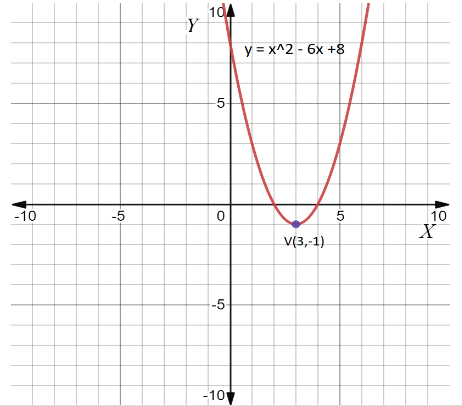
Note : We need to find the vertex from the equation of parabola and substitute the given values into the function and plot a graph with respect to the function and the point. We need to remember the concept to solve the problems with different values.a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.