Question

How do you find the vertex and the intercepts for $y = {x^2} + 8x + 15$ ?

Answer 1

The equation of the form ${(x - h)^2} = 4p(y - k)$ is the equation of a parabola. The value of $x$ - coordinate of the vertex = $- \dfrac{b}{{2a}}$ and putting this value of $x$ in the given equation, value of the $y$ coordinate of the vertex can be determined.

Complete step-by-step solution:
Let $y = {x^2} + 8x + 15$ be considered as $y = a{x^2} + bx + c$
Now, $x$ coordinate of vertex will be given by $- \dfrac{b}{{2a}}$ , i.e., $x$ coordinate of vertex = $- \dfrac{8}{2} = - 4$
Therefore, $y$ -coordinate of the vertex will be (substituting the $x$ coordinate in the equation)
$\Rightarrow y = {( - 4)^2} + 8( - 4) + 15$
$\Rightarrow y = - 1$
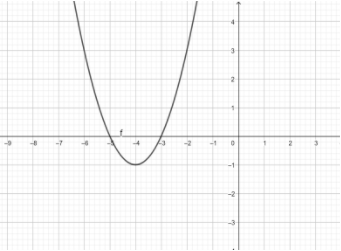
Hence, coordinates of the vertex are $\left( { - 4, - 1} \right)$ .
To find the $y$ -intercept, put $x = 0$ in the equation;
Hence, $y$ intercept=15.
To find the $x$ -intercept, put $y = 0$ in the equation
${x^2} + 8x + 15 = 0$
The above equation becomes a quadratic equation. We need to find the roots of this equation. Roots are those values for which the equation returns zero as a value. This equation can be written as
$\Rightarrow {x^2} + (3 + 5)x + (3 \times 5) = 0$
Splitting the middle term so that we can find common and regroup them, we get,
$\Rightarrow {x^2} + 3x + 5x + 15 = 0$
Taking common and regrouping
$\Rightarrow x(x + 3) + 5(x + 3) = 0$
Making factors,
$\Rightarrow (x + 3)(x + 5) = 0$
Keeping each factor equal to 0,
$\Rightarrow x + 3 = 0$
$\Rightarrow x = - 3$
Now, we will keep another factor equal to 0,
$\Rightarrow x + 5 = 0$
$\Rightarrow x = - 5$
Finding the roots of the above equation we get,
$x = - 3$ and $- 5$ .
Hence, intercepts of $x$ will be $- 3$ and $- 5$. Hence, now we will plot these points on the graph.

Note: A parabola is a curve which is equidistant from a fixed point (called the focus) and a straight line (called the directrix).
The general equation of a parabola is of the form, $y = {x^2}$ , when the vertex is at the origin $(0,0)$ . The vertex is the point where the parabola is the sharpest.
${(x - h)^2} = 4p(y - k)$ is the equation of a parabola with vertex not at origin. The coordinates of the vertex are $(h,k)$ . Axis of symmetry is determined by the value $x = h$ .
The term $p$ determines whether the parabola will be opening upwards or downwards. If $p > 0$ , parabola opens upwards, else if, $p < 0$ , parabola opens downwards.