Question

How do you find the vertex and axis of symmetry, and intercepts for a quadratic equation $y={{x}^{2}}+6x+5$ ?

Answer 1

From the given question we have been asked to find the vertex, axis of symmetry and intercepts of the parabola $y={{x}^{2}}+6x+5$. So, for this question we will take the help of the vertex form of the parabola and reduce our given equation into this form and find the vertex, axis of symmetry. For finding the intercepts we will use a substitution method and find the both intercepts.

Complete step by step solution:
Firstly, we will use the vertex form of parabola which is given as follows.
$\Rightarrow y=a{{\left( x-h \right)}^{2}}+k$
Here, the point $(h,k)$ is the vertex of the parabola.
The axis of symmetry will be as follows.
$\Rightarrow x=h$
So, now we will reduce the given equation into the vertex form using the completing square method. So we get,
$\Rightarrow y={{x}^{2}}+6x+5$
The standard form for the completing square method is $a{{x}^{2}}+bx+c=0$.
So, by comparing the given equation we get,
$\Rightarrow a=1,b=6,c=5$
So, in the step one we will move the constant to the other side of the equation.
$\Rightarrow {{x}^{2}}+6x+5=0$
$\Rightarrow {{x}^{2}}+6x=-5$
Now, we will add $3$ square on both sides. So, we get,
$\Rightarrow {{x}^{2}}+6x+9=-5+9$
$\Rightarrow {{x}^{2}}+6x+9=4$
Now, the expression in the left hand side of the equation can be written as a perfect square as follows.
$\Rightarrow {{\left( x+3 \right)}^{2}}=4$
Now, we will send the four to other side to get the vertex form.
$\Rightarrow {{\left( x+3 \right)}^{2}}-4=0$
So, when we compare with vertex form $\Rightarrow y=a{{\left( x-h \right)}^{2}}+k$. We get,
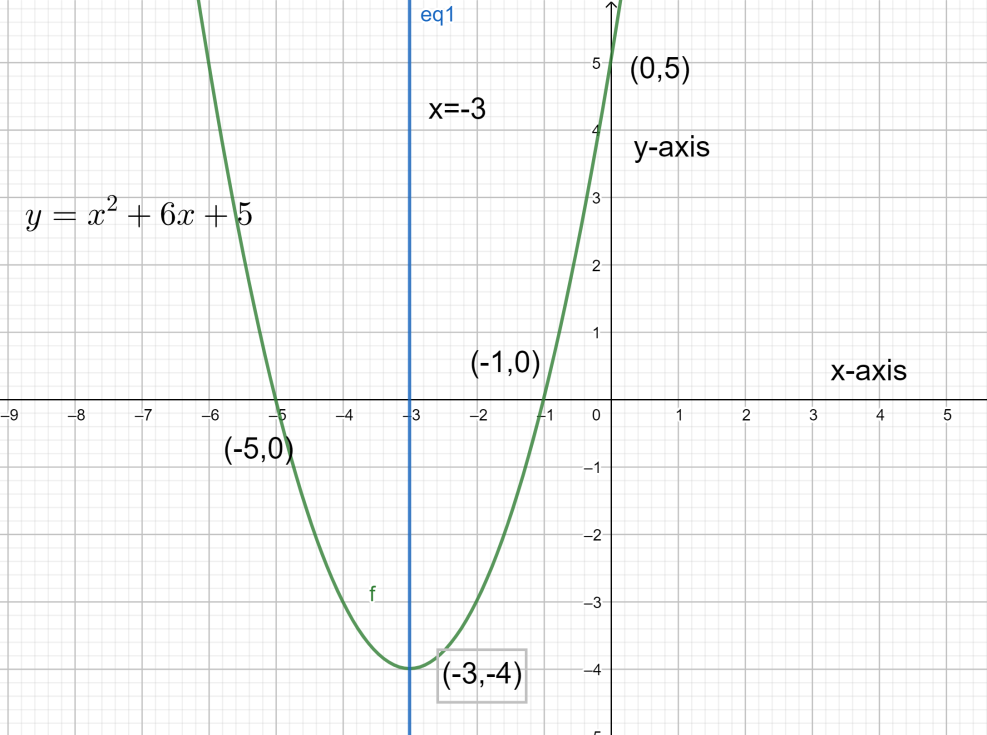
Hence, vertex is $\Rightarrow \left( -3,-4 \right)$.
The axis of symmetry will be as follows.
$\Rightarrow x=h$
$\Rightarrow x=-3$
Now, we find the x and y intercepts using substitution method.
We substitute $y=0$ and find the x intercepts. So, we get,
$\Rightarrow {{x}^{2}}+6x+5=0$
We split the middle term into terms as follows.
$\Rightarrow {{x}^{2}}+5x+x+5=0$
Now, we take x common. We get,
$\Rightarrow x(x+5)+x+5=0$
$\Rightarrow \left( x+5 \right)\left( x+1 \right)=0$
$\Rightarrow x=-1,-5$
Now, we get x intercepts as follows.
$\Rightarrow \left( -1,0 \right)$ and $\Rightarrow \left( -5,0 \right)$.
Now, we find y intercept by substituting x as zero.
$\Rightarrow y={{x}^{2}}+6x+5$
$\Rightarrow y=5$
So, the y intercept will be $\Rightarrow \left( 0,5 \right)$.
The graph for the question will be as follows.

Note: Students must have good knowledge in the concept of parabola and its applications. Students must be able to do the complete square method without any calculation mistakes. Students must know the vertex form of parabola which is as follows.
$\Rightarrow y=a{{\left( x-h \right)}^{2}}+k$.
The vertex for this form as $(h,k)$ and the axis of symmetry will be $\Rightarrow x=h$.