Question
Question: How do you find the value of \[{\sin ^{ - 1}}(\dfrac{3}{5})\]?...
How do you find the value of sin−1(53)?
Solution
We will use the trigonometric identity cos2+sin2=1. We will use the Pythagoras theorem here, i.e. sinθ=HP and cosθ=HB where P means perpendicular, B is base and H means hypotenuse. The inverse of sin function is denoted by Arcsine or sin−1
Complete step by step answer:
Let, sin−1(53)=θ
⇒sinθ=53
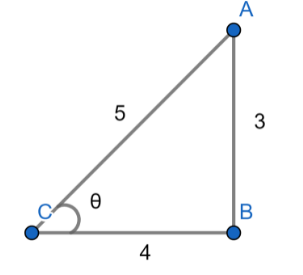
So the value of θwill be 2−π⩽θ⩽2π
Since, we know that, cosθ=HB
where B is the base and H is the hypotenuse.
From the above diagram, the value of cos will be,
cosθ=54
Another method to solve this is by using trigonometry identity.
sinθ=53
So, apply the trigonometry identity here i.e.
cos2θ=1−sin2θ
Taking square root on both the sides, we get,
⇒cosθ=1−sin2θ
Substituting the value, we get,
⇒cosθ=1−(53)2
Removing the brackets, we get,
⇒cosθ=1−259
Simplify the above equation, we get,
⇒cosθ=2525−9
⇒cosθ=2516
⇒cosθ=(54)2
∴cosθ=54
Note: The expression sin−1(x)is not the same as sin(x)1. In other words, −1 is not an exponent. Instead, it simply means inverse function. The trigonometric functions sinx, cosx and tanx can be used to find an unknown side length of a right triangle, if one side length and an angle measure are known. The inverse trigonometric functions sin−1x,cos−1x,tan−1x, are used to find the unknown measure of an angle of a right triangle when two side lengths are known. Pythagoras’ Theorem describes the mathematical relationship between three sides of a right-angled triangle. Trigonometry is a field of study in mathematics which observes the relationships of the sides and angles of triangles. The symbol θ is used to describe an unknown angle. These functions are defined as the ratios of the different sides of a triangle.
