Question

How do you find the value of five trigonometric functions of the acute angle with $\sec A = \dfrac{7}{3}$ ?

Answer 1

Hint : We are given with one trigonometric function. Also the value for each function is given. We will use the value to obtain the other trigonometric functions. Because we know the ratio of the trigonometric functions can be obtained by the base, height and hypotenuse of a right angle triangle. So we will first obtain the value of these three terms and then use them in obtaining the other trigonometric functions.

Complete step by step solution:
Given that $\sec A = \dfrac{7}{3}$
But we know that $\sec A = \dfrac{{hypotenuse}}{{adj.side}}$
So we get, $hypotenuse = 7$ and $adjecent = 3$
So using Pythagoras theorem we get,
$opp.side = \sqrt {{7^2} - {3^2}} = \sqrt {49 - 9} = \sqrt {40}$
This is the value of the opposite side.

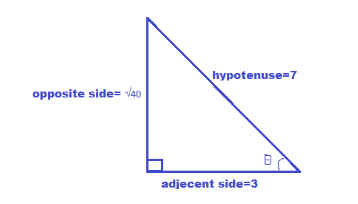
Now we will obtain the remaining trigonometric functions with the help of the ratio of their sides.
$\sin A = \dfrac{{opp.side}}{{hypotenuse}} = \dfrac{{\sqrt {40} }}{7}$
$\cos A = \dfrac{{adj.side}}{{hypotenuse}} = \dfrac{3}{7}$
$\tan A = \dfrac{{opp.side}}{{adj.side}} = \dfrac{{\sqrt {40} }}{3}$
$\cot A = \dfrac{{adj.side}}{{opp.side}} = \dfrac{3}{{\sqrt {40} }}$
$\cos ecA = \dfrac{{hypotenuse}}{{opp.side}} = \dfrac{7}{{\sqrt {40} }}$
These are the trigonometric functions and their values so obtained.

Note : Here note that we are asked to find the remaining ratios from the given trigonometric function and not the angle. We may get confused and try to find the acute angle but we don’t need it.
Also note that if we do not want to find the sides of the right angled triangle we can use standard trigonometric identities to find the remaining functions.
Like from the sec function we can find the value of cos. Then from the cos function we can find sin. Then after that we can find the remaining functions also.