Question

How do you find the value of $\csc ,\sec$, and $\cot$ of theta in a unit circle?

Answer 1

Here we will first draw a circle with radius 1. Then by taking any one of the quadrants we will form a triangle in it. Finally, by using the basic formula of trigonometric angles we get the required value of the trigonometric functions.

Complete step-by-step answer:
First, as the radius of the circle is given 1 unit, we will draw a circle with radius one as,

Next, as we have to find the value of trigonometric identities we will form a triangle ABC inside the circle as,

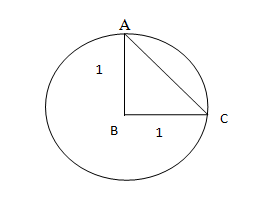
As $AB$ and$BC$are the radii of the circle their value is 1.
Using Pythagoras theorem, we get
$A{C^2} = A{B^2} + B{C^2}$
Substituting $AB = 1$ and $BC = 1$ in the above equation, we get
$\begin{array}{l} \Rightarrow A{C^2} = {1^2} + {1^2}\\\ \Rightarrow A{C^2} = 1 + 1\end{array}$
Adding the terms, we get
$\Rightarrow AC = \sqrt 2$
So, we get our diagram as,

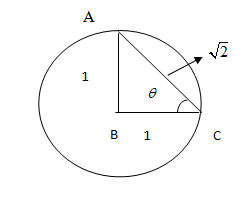
Next, we know
1. $\sin \theta =$ Perpendicular $\div$ Hypotenuse
$\Rightarrow \sin \theta = \dfrac{{AB}}{{AC}} = \dfrac{1}{{\sqrt 2 }}$
We know that $\csc \theta = \dfrac{1}{{\sin \theta }}$.
$\csc \theta = \dfrac{1}{{\dfrac{1}{{\sqrt 2 }}}} = \sqrt 2$
2. $\cos \theta =$ Base $\div$ Hypotenuse
$\Rightarrow \cos \theta = \dfrac{{BC}}{{AC}} = \dfrac{1}{{\sqrt 2 }}$
We know that $\sec \theta = \dfrac{1}{{\cos \theta }}$.
$\sec \theta = \dfrac{1}{{\dfrac{1}{{\sqrt 2 }}}} = \sqrt 2$
3. $\cot \theta = \dfrac{{\cos \theta }}{{\sin \theta }}$
Substituting $\sin \theta = \dfrac{1}{{\sqrt 2 }}$ and $\cos \theta = \dfrac{1}{{\sqrt 2 }}$ in the above equation, we get
$\cot \theta = \dfrac{{\dfrac{1}{{\sqrt 2 }}}}{{\dfrac{1}{{\sqrt 2 }}}} = \dfrac{{\sqrt 2 }}{{\sqrt 2 }} = 1$

Therefore, we get the value of $\csc \theta ,\sec \theta$ and $\cot \theta$ in a unit circle as $\sqrt 2 ,\sqrt 2$ and 1 respectively.

Note:
Trigonometry is a branch of mathematics that deals with specific functions of angles and also their application in calculations and simplification. The commonly used six types of trigonometry functions are defined as sine, cosine, tangent, cotangent, secant, and cosecant. Identities are those equations that are true for every variable. Reciprocal identities are used to cover the base of inverse values where cosecant is reciprocal of sine, secant is reciprocal of cosine and cotangent is reciprocal of a tangent.