Question

How do you find the value of $\csc 30^\circ$?

Answer 1

Start with assuming an equilateral triangle $\Delta MNP$ and make a perpendicular MO which divides the side NP into two equal parts NO and OP. This gives you $\angle PMO = 30^\circ$ . Now use the definition of the cosecant function, find the expression for it. Now substitute the values in it and simplify it to get the required value of $\csc 30^\circ$.

Complete step-by-step answer:
Here in this question, we are given an expression in the cosecant function, i.e. $\csc 30^\circ$ and we have to find the value for this expression.
Before starting with the solution, we must understand a few concepts about cosine functions. Csc or Cosec function (or cosecant function) in a triangle is the ratio of the hypotenuse to that of perpendicular. It is the reciprocal of the sine function by value. The sine function is one of the three main primary trigonometric functions.
For finding this value, we first take an equilateral triangle $\Delta MNP$ with a side of length ‘m’ units. In this triangle, we have a perpendicular bisector $MO$, that divides side NP into two equal parts. We know that an equilateral has all three interior angles equal and of measure $60^\circ$.
$\Rightarrow NO = OP = \dfrac{{NP}}{2} = \dfrac{m}{2}$ and $\angle PMO = \dfrac{{\angle PMN}}{2} = \dfrac{{60^\circ }}{2} = 30^\circ$
This information can be represented in a diagram as:

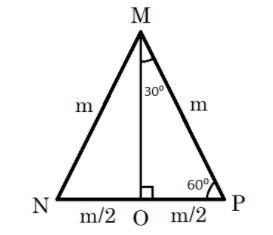
Now taking the right-angle triangle $\Delta PMO$ into consideration, we know that $PM = m{\text{ and }}OP = \dfrac{m}{2}$
We can use the Pythagoras theorem, which states that the square of the length of the hypotenuse of a right triangle equals the sum of the squares of the lengths of the other two sides. By this theorem, in the triangle $\Delta PMO$, we get:
$\Rightarrow P{M^2} = M{O^2} + O{P^2}$
Now let’s substitute the known values in this equation:
$\Rightarrow P{M^2} = M{O^2} + O{P^2} \Rightarrow {m^2} = M{O^2} + {\left( {\dfrac{m}{2}} \right)^2}$
This equation can be easily solved to find the unknown length of perpendicular MO
$\Rightarrow {m^2} = M{O^2} + {\left( {\dfrac{m}{2}} \right)^2} \Rightarrow M{O^2} = {m^2} - \dfrac{{{m^2}}}{4} = \dfrac{{3{m^2}}}{4}$
Taking square root on both the sides, we have:
$\Rightarrow \sqrt {M{O^2}} = \sqrt {\dfrac{{3{m^2}}}{4}} \Rightarrow MO = \dfrac{{\sqrt 3 }}{2}m$
Therefore, we get the length of the perpendicular MO as $\dfrac{{\sqrt 3 }}{2}m$
Now, according to the definition of the cosec function, we have the relation:
$\Rightarrow \cos ec\theta = \dfrac{1}{{\sin \theta }} = \dfrac{{Hypotenuse}}{{Perpendicular}}$
For the triangle $\Delta PMO$, using cosine function in angle $\angle PMO$, we can write it as:
$\Rightarrow \cos ec\theta = \dfrac{1}{{\sin \theta }} = \dfrac{{Hypotenuse}}{{Perpendicular}} = \dfrac{{MP}}{{OP}} = \dfrac{m}{{\dfrac{m}{2}}}$
This can be simplified by dividing numerator and denominator by ‘m’
$\Rightarrow \cos ec30^\circ = \dfrac{m}{{\dfrac{m}{2}}} = 2$

Therefore, we get the required value of $\cos ec30^\circ$ or $\csc 30^\circ$ as $2$

Note: In this question, we used an example of an equilateral triangle that was a crucial part of the solution. Notice that the value of $\csc 30^\circ$ does not depend on the sides of the triangle, i.e. ‘m’. An alternative approach to this problem can be to find the value of $\sin 30^\circ$ and then use the relation $\csc \theta = \dfrac{1}{{\sin \theta }}$.