Question

How do you find the value of $\cos \left( {\dfrac{\pi }{2}} \right)$ using graph of “cosx”?

Answer 1

Hint : Here the given question need to be solved using the graph of “cosx”, here we have to first plot the graph of cosx and then see the value for the given angle which is ninety degree, to cross check the answer we can direct see the value of the cosx trigonometric function which we know already and is zero.
Formulae Used:
$\Rightarrow \cos \left( {\dfrac{\pi }{2}} \right) = 0$ we know value of trigonometric function “cosx” for ninety degree angle is zero.

Complete step-by-step answer :
Here the given question need us to find the value for the cosx function for the given angle ninety with the help of the graph, here we have to plot the graph of cosx in which x-axis will denote the angles and y-axis will denote the value for the given angle, and hence the value at ninety degree will be our required answer for the give question, on [plotting we get:

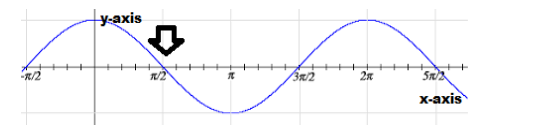
Here in the graph we can see the value of the trigonometric function “cos” for ninety degree angles is zero.

Note : The above question need us to find the value for “cosx” for the given angle, here we have to know the graph of the given function in order to find the value for the angles given, without knowledge of graph we cannot solve this by using graph method, else we have to direct give the answer as we know the values for the standard trigonometric angles, with the functions.