Question

How do you find the value of $c$ such that $y=\dfrac{3}{2}x+6$ is tangent to the curve $y=c\sqrt{x}$?

Answer 1

In this problem we have given the equation of the tangent to a curve and asked to calculate the constant value in the curve equation which is $c$. We know that the slope of the tangent and the slope of the curve at tangent point are equal. But here we don’t have the tangent point. So, we will calculate the derivative of the given curve and equate it to the slope of the tangent. Here we will get an equation. Now we will observe all the equations we have and use proper substitutions to solve them. After solving the equations, we will get the coordinates of the tangent point. Now we will use the coordinates of the tangent point to get the value of $c$.

Complete step by step solution:
Given that, $y=\dfrac{3}{2}x+6$ is tangent to the curve $y=c\sqrt{x}$.
Considering the equation of the curve which is $y=c\sqrt{x}$.
Differentiating the above equation with respect to $x$, then we will get
$\begin{aligned} & \Rightarrow \dfrac{dy}{dx}=\dfrac{d}{dx}\left( c\sqrt{x} \right) \\\ & \Rightarrow \dfrac{dy}{dx}=c\dfrac{d}{dx}\left( \sqrt{x} \right) \\\ \end{aligned}$
We have the differentiation formula $\dfrac{d}{dx}\left( \sqrt{x} \right)=\dfrac{1}{2\sqrt{x}}$. Substituting this value in the above equation, then we will get
$\Rightarrow \dfrac{dy}{dx}=\dfrac{c}{2\sqrt{x}}$
Considering the equation of the tangent which is $y=\dfrac{3}{2}x+6$.
The given tangent is in the form of slope intercept form i.e., $y=mx+c$, where $m$is the slope of the line. So, comparing the given tangent equation with $y=mx+c$, then we will get slope of the tangent as
$m=\dfrac{3}{2}$.
Equating the above slope value with the derivative of the curve, then we will get
$\begin{aligned} & \Rightarrow \dfrac{c}{2\sqrt{x}}=\dfrac{3}{2} \\\ & \Rightarrow c=3\sqrt{x} \\\ \end{aligned}$
In this problem up to now we have the equations $c=3\sqrt{x}$, $y=\dfrac{3}{2}x+6$, $y=c\sqrt{x}$. By observing the all the above equations, we are going to substitute $c$ value in equation of curve and then equate it to equation of tangent, then we will get
$\Rightarrow 3\sqrt{x}\sqrt{x}=\dfrac{3}{2}x+6$
We know that $\sqrt{x}\sqrt{x}=x$, then we will have
$\Rightarrow 3x=\dfrac{3}{2}x+6$
Simplifying the above equation, then we will get
$\begin{aligned} & \Rightarrow 3x=3\left( \dfrac{x}{2}+2 \right) \\\ & \Rightarrow x=\dfrac{x}{2}+2 \\\ & \Rightarrow x-\dfrac{x}{2}=2 \\\ & \Rightarrow x=4 \\\ \end{aligned}$
Substituting this value in the equation $c=3\sqrt{x}$, then we will get
$\begin{aligned} & \Rightarrow c=3\sqrt{4} \\\ & \Rightarrow c=3\times 2 \\\ & \Rightarrow c=6 \\\ \end{aligned}$
Hence the value of $c$ is $6$, from this the equation of the curve will be $y=6\sqrt{x}$. Now the graph of the curve and the tangent will be

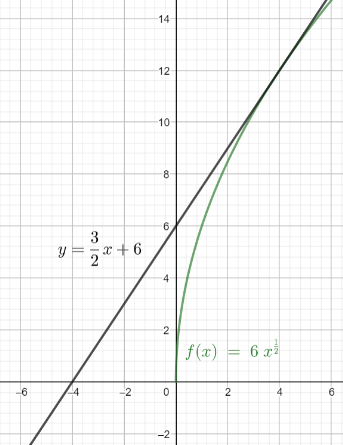
Note: In this problem they have not asked to calculate the tangent point, so we have just calculated the $x$ coordinate of the point in the above solution. If they have asked to calculate the tangent point, then we will substitute the calculated $x$ value in either equation of the tangent or equation of curve.