Question

How do you find the terminal point $p\left( {x,y} \right)$ on the unit circle determined by the giving value of $t = \dfrac{{ - 3\pi }}{4}$ ?

Answer 1

Hint : In order to find the terminal point $p\left( {x,y} \right)$ on the unit circle, start with $\left( {1,0} \right)$ which is $\left( {\cos {0^ \circ },\sin {0^ \circ }} \right)$ at ${0^ \circ }$ , as we know that the general terminal point for a circle is $p\left( {\cos x,\sin x} \right)$ . We are given with the angle of $t = \dfrac{{ - 3\pi }}{4}$ . So just put the value of $t$ in the place of $x$ in $p\left( {\cos x,\sin x} \right)$ solve and get the value in the form of $p\left( {x,y} \right)$ , where $p\left( {x = \cos x,y = \sin x} \right)$ .

Complete step by step solution:
We are given with the angle $t = \dfrac{{ - 3\pi }}{4}$ .
Since, we know that the general terminal point of a unit circle is: $p\left( {\cos x,\sin x} \right)$ .
Representing it in diagram we get:

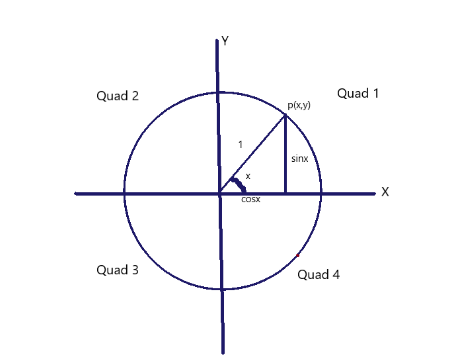
Put the value of $t = \dfrac{{ - 3\pi }}{4}$ , in the place of $x$ and we get:
$p\left( {x = \cos x,y = \sin x} \right) = p\left( {\cos \left( {\dfrac{{ - 3\pi }}{4}} \right),\sin \left( {\dfrac{{ - 3\pi }}{4}} \right)} \right)$
Solving each part of sine and cosine separately:
As we know that $\cos \left( { - x} \right)$ is written as $\cos x$ , with this for cosine we can write:
$\cos \left( {\dfrac{{ - 3\pi }}{4}} \right) = \cos \left( {\dfrac{{3\pi }}{4}} \right)$
Solving it for simplest form, to know the value we write:
$\cos \left( {\dfrac{{3\pi }}{4}} \right) = \cos \left( {\pi - \dfrac{\pi }{4}} \right)$
As this would give the value of cosine in 2nd Quadrant which is not the home of cosine so the value will be negative and we also know that $\cos \left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}$.Putting it in the value and we get: $\cos \left( {\pi - \dfrac{\pi }{4}} \right) = - \cos \left( {\dfrac{\pi }{4}} \right) = - \dfrac{1}{{\sqrt 2 }}$
Similarly solving for sine, we get:
$\sin \left( {\dfrac{{ - 3\pi }}{4}} \right) = - \sin \left( {\dfrac{{3\pi }}{4}} \right)$
Solving it for simplest form, to know the value we write:
$- \sin \left( {\dfrac{{3\pi }}{4}} \right) = - \sin \left( {\pi - \dfrac{\pi }{4}} \right)$
As this would give the value of sine in 2nd Quadrant which is the home of sine so the value will be positive and we also know that $\sin \left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}$.Putting it in the value and we get: $- \sin \left( {\pi - \dfrac{\pi }{4}} \right) = - \sin \left( {\dfrac{\pi }{4}} \right) = - \dfrac{1}{{\sqrt 2 }}$
Hence, $p\left( {\cos x,\sin x} \right)$ becomes $p\left( {\cos \left( {\dfrac{{ - 3\pi }}{4}} \right),\sin \left( {\dfrac{{ - 3\pi }}{4}} \right)} \right) = p\left( { - \dfrac{1}{{\sqrt 2 }}, - \dfrac{1}{{\sqrt 2 }}} \right)$
Therefore, the terminal point $p\left( {x,y} \right)$ on the unit circle determined by the giving value of $t = \dfrac{{ - 3\pi }}{4}$ is: $p\left( {\cos \left( {\dfrac{{ - 3\pi }}{4}} \right),\sin \left( {\dfrac{{ - 3\pi }}{4}} \right)} \right) = p\left( { - \dfrac{1}{{\sqrt 2 }}, - \dfrac{1}{{\sqrt 2 }}} \right)$ where $x = \cos \left( { - \dfrac{{3\pi }}{4}} \right) = - \dfrac{1}{{\sqrt 2 }}$ and $y = \sin \left( { - \dfrac{{3\pi }}{4}} \right) = - \dfrac{1}{{\sqrt 2 }}$ .
So, the correct answer is “$p\left( { - \dfrac{1}{{\sqrt 2 }}, - \dfrac{1}{{\sqrt 2 }}} \right)$ ”.

Note : Always check for the Quadrants for the sign of the values.
If the angle is positive then move counter clockwise also called anti-clockwise, and if angle is negative then move clockwise.