Question

How do you find the standard form of $5{x^2} + 8{y^2} + 16y - 32 = 0$ and what kind of a conic is it?

Answer 1

Hint : To solve the given equation, we need to apply completing the square method, such that we get the form of ${\left( {a + b} \right)^2}$ , and then on further simplification we get the standard form of the given equation. Completing the square method is one of the methods to find the roots of the given quadratic equation and a polynomial equation with degree equal to two is known as a quadratic equation.

Complete step by step solution:
Let us write the given equation:
$5{x^2} + 8{y^2} + 16y - 32 = 0$
As, y term is common in the given equation, hence let us combine the terms and rewrite the equation as:
$5{x^2} + 8\left( {{y^2} + 2y} \right) = 32$
Now, let us apply complete the square method as:
$5{x^2} + 8\left( {{y^2} + 2y + 1} \right) = 32 + 8$
As in the obtained equation, we have the expansion of ${\left( {a + b} \right)^2}$ as ${\left( {y + 1} \right)^2} = {y^2} + 2y + 1$ , hence we get:
$\Rightarrow 5{x^2} + 8{\left( {y + 1} \right)^2} = 40$
Now, divide both sides of the equation by 40
$\dfrac{{5{x^2}}}{{40}} + \dfrac{{8{{\left( {y + 1} \right)}^2}}}{{40}} = \dfrac{{40}}{{40}}$
Simplifying the terms, we get the standard form as:
$\Rightarrow \dfrac{{{x^2}}}{8} + \dfrac{{{{\left( {y + 1} \right)}^2}}}{5} = 1$
This is an ellipse since the coefficients on x and y are different, the center $= \left( {0, - 1} \right)$ and the major axis is horizontal.

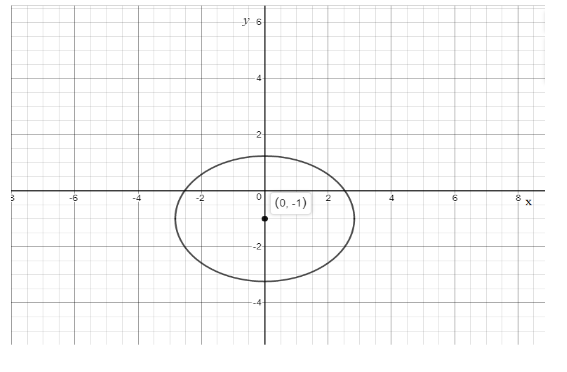
Note : We have used Completing the square of a substitution in order to reduce a polynomial equation to simpler form. And as we got the conic as Ellipse, as we know that an ellipse is the locus of all those points in a plane such that the sum of their distances from two fixed points in the plane is constant. An ellipse is formed when a cone is intersected by a plane at an angle with respect to its base and it has two focal points and the sum of the two distances to the focal point, for all the points in the curve, is always constant.