Question

How do you find the slope perpendicular to $y=2$ ?

Answer 1

To find the slope of a line with respect to the slope of another line, first write the equation of the given line in the slope-intercept form, and then if the lines are perpendicular to each other then use the formula ${{m}_{1}}{{m}_{2}}=-1$ to find the slope of the other line.

Complete step-by-step answer:
Given the line:
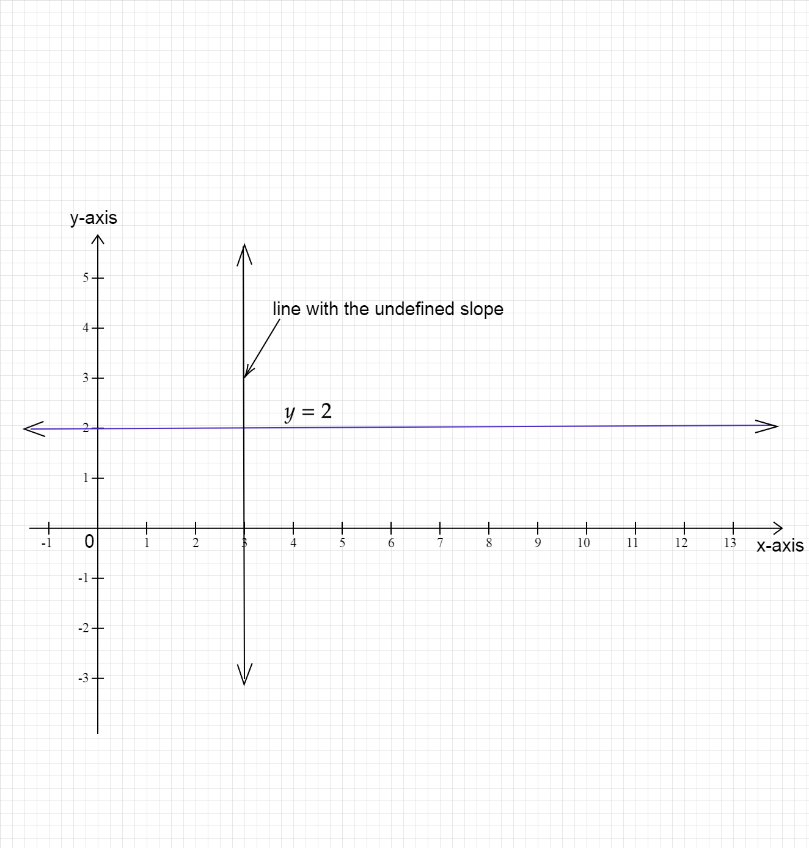
$\Rightarrow y=2$
When two lines are perpendicular then their slopes satisfy the condition ${{m}_{1}}{{m}_{2}}=-1$ where ${{m}_{1}}$and ${{m}_{2}}$ represent the slopes of the given two lines respectively.
Also, by definition of a horizontal line, we can say that the slope of a horizontal line is zero. For a line perpendicular to a horizontal line, the slope of it will be undefined as a line perpendicular to a horizontal line will be a vertical line.
Writing the given equation in the form of slope-intercept form we get,
$\Rightarrow y=0x+2$ , where we can see that the slope of the given line is $0$ . This concludes that the given line is a horizontal line and is parallel to the $x$- axis.
Now, to find a line that has the slope perpendicular to this line substitute the value of the slope of line 1 in the formula${{m}_{1}}{{m}_{2}}=-1$.
So, we get the slope of the second line as,
$\Rightarrow 0\times {{m}_{2}}=-1$
$\Rightarrow {{m}_{2}}=\dfrac{-1}{0}=\infty$
Therefore, we get the slope perpendicular to $y=2$ as undefined.

Note: A slope or gradient of a line can be defined as the value or number that denotes the direction and the steepness of the given line. The slope is generally represented by the letter $m$ . A slope can be calculated by calculating the ratio of the change vertically to the horizontal change between any two distinct points on a given line.