Solveeit Logo
Login

Question

Question: how do you find the slope of the secant lines of \[f(x) = 6x - 1{x^2}\] through the points \[(2,f(2)...

how do you find the slope of the secant lines of f(x)=6x−1x2f(x) = 6x - 1{x^2} through the points (2,f(2))(2,f(2)) and (2+h,f(2+h))(2 + h,f(2 + h))?

Explanation

Solution

First, we will use the formula of the gradient to find slope. We will put the points in the formula and try to simplify it. After that we will put the value of f(x) in that solving part and try to solve them, this will give us our answer.

Formula used: m=y2−y1x2−x1m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}

Complete step by step answer:
Slope also means gradient here.
According to this question, we have to find the slope by using the two points. Here, we will use the gradient formula to find the slope or gradient. The formula is:
m=y2−y1x2−x1m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}
In this formula, (x1,y1)  and  (x2,y2)({x_1},{y_1})\,\,and\,\,({x_2},{y_2}) are the points. So, according to the question, we get:
(x1,y1)=(2,f(2))({x_1},{y_1}) = (2,f(2)) and (x2,y2)=(2+h,f(2+h))({x_2},{y_2}) = (2 + h,f(2 + h))
Now, we will put the values or points in the formula, and we get:
⇒m(h)=f(2+h)−f(2)2+h−2\Rightarrow m(h) = \dfrac{{f(2 + h) - f(2)}}{{2 + h - 2}}
Now, we will substitute the values 6x−x26x - {x^2} in the solving part, and we get:
⇒m(h)=(6−(2+h))(2+h)−(6×2−22)2+h−2\Rightarrow m(h) = \dfrac{{(6 - (2 + h))(2 + h) - (6 \times 2 - {2^2})}}{{2 + h - 2}}
Now, we will simplify the denominator, and we get:
⇒m(h)=(6−(2+h))(2+h)−(6×2−22)h\Rightarrow m(h) = \dfrac{{(6 - (2 + h))(2 + h) - (6 \times 2 - {2^2})}}{h}
Now, we will simplify the numerator, and we get:
⇒m(h)=(4−h)(2+h)−(12−4)h\Rightarrow m(h) = \dfrac{{(4 - h)(2 + h) - (12 - 4)}}{h}
⇒m(h)=4(2+h)−h(2+h)−8h\Rightarrow m(h) = \dfrac{{4(2 + h) - h(2 + h) - 8}}{h}
⇒m(h)=8+4h−2h−h2−8h\Rightarrow m(h) = \dfrac{{8 + 4h - 2h - {h^2} - 8}}{h}
⇒m(h)=2h−h2h\Rightarrow m(h) = \dfrac{{2h - {h^2}}}{h}
Now, we will take hhcommon here, and we get:
⇒m(h)=h(2−h)h\Rightarrow m(h) = \dfrac{{h(2 - h)}}{h}
Now, the common terms from the numerator and denominator get cancelled. Here, hh gets cancelled from both numerator and denominator, and we get:
⇒m(h)=(2−h)\Rightarrow m(h) = (2 - h)
Therefore, we get the slope as (2−h)(2 - h).
If we calculate by taking limit, then lim⁡h→0 m(h)=lim⁡h→0 2−h\mathop {\lim }\limits_{h \to 0} \,m(h) = \mathop {\lim }\limits_{h \to 0} \,2 - h. We get our answer as 22. This is the coefficient of the tangent line to f(x)f(x) at the point 22.

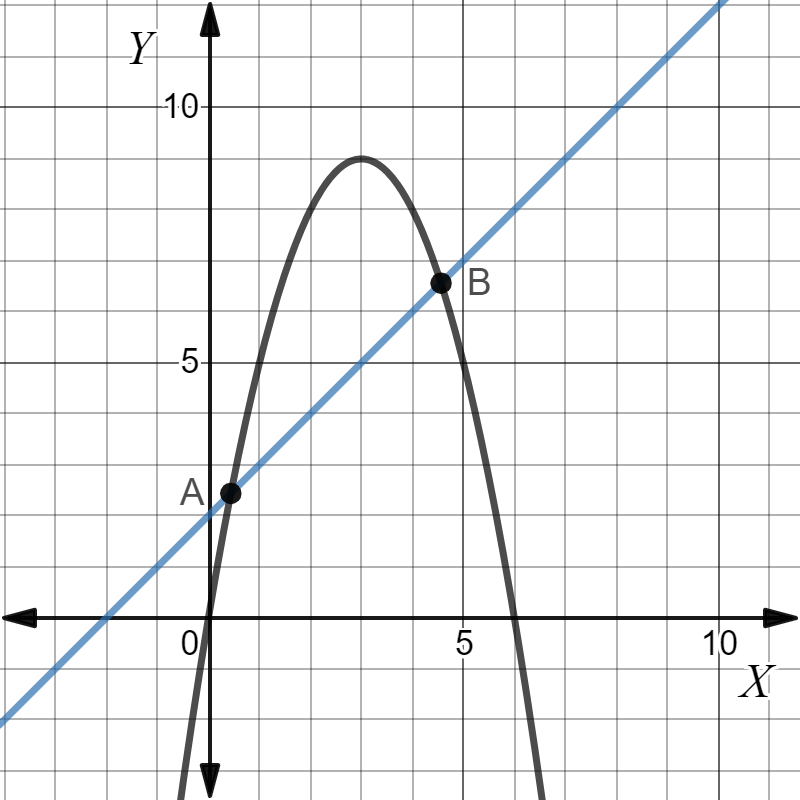
Note: While plotting a graph, when we draw a line on that graph of curve, if the line intersects that curve at two or more than two points, then that line is a secant line, as we can see in the following graph, the blue line is a secant to the curve because it is intersecting the curve twice at “A” and “B”