Question

How do you find the slope of the line $x-4y=8$?

Answer 1

If the degree of an equation is one, then it is a linear equation. The graph of a linear equation is a straight line. The standard form of the equation of the straight line is $ax+by+c=0$. We can find the slope intercepts of the line using the coefficients of the equation of the straight line. The slope of the straight line is $\dfrac{-a}{b}$, we can find the slope by substituting the values of coefficients of the straight line equation.

Complete step by step solution:
We are given an equation of the straight line $x-4y=8$, we need to find the slope of this line. Subtracting 8from both sides of the above equation, it can be expressed as, $x-4y-8=0$. We know that the standard form of the equation of the straight line is $ax+by+c=0$. The slope of the straight line is $\dfrac{-a}{b}$. Comparing the given equation with the standard form of straight line, we get $a=1,b=-4\And c=-8$.
Thus, we can find the slope of the given straight line as $slope=\dfrac{-a}{b}$. Substituting the values, we get
$\Rightarrow slope=\dfrac{-1}{-4}=\dfrac{1}{4}$
Thus, the slope of the straight line is $\dfrac{1}{4}$.
We can also plot the graph of the straight line using the given equation as,

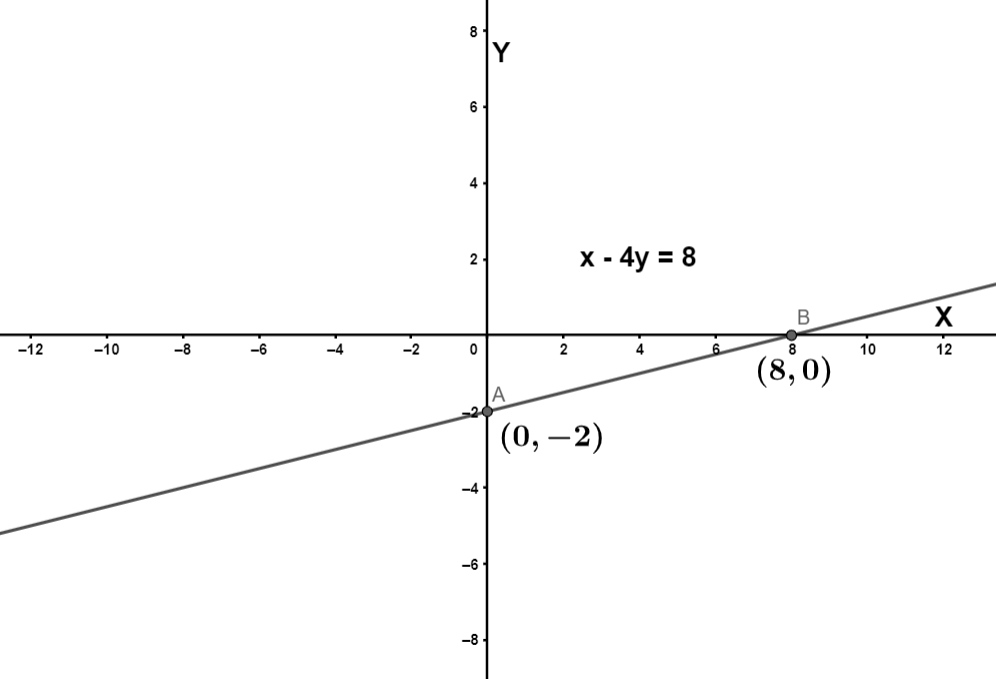
Note: We can also use the slope-intercept form of the equation of straight line to find the slope, the slope-intercept form is $y=mx+c$, here m is the slope of the line, and c is its Y-intercept. To convert it to this form, we need to take y to one side of the equation and make its coefficient equals to one.