Question

How do you find the slope of the line through the points $\left( 6,-6 \right)\And \left( 4,5 \right)$?

Answer 1

We want to find the slope of the straight line, so we should use the slope-intercept form of the equation of the straight line. The slope-intercept form of a straight line is $y=mx+c$, here m is the slope of the straight line, and c is the Y-intercept. We are given two points through which the line passes, so these two points must satisfy the equation of the straight line. After substituting, we will get two linear equations in c, and m. we can solve these equations to find the value of m, that is the slope of the straight line.

Complete step by step answer:
The equation of a straight line in slope-intercept form is $y=mx+c$ , here m is the slope of the line and c is the Y-intercept. We are given that the line passes through the points $\left( 6,-6 \right)\And \left( 4,5 \right)$. As the line passes through these points, they must satisfy the equation of the straight line.
Substituting $\left( 6,-6 \right)$ in the equation of the straight line, we get $-6=6m+c$. Substituting $\left( 4,5 \right)$ in the equation of the straight line, we get $5=4m+c$. We get the two equations. We can find the slope by solving them.
Subtracting the first equation from the second, we get
$\Rightarrow 11=-2m$
Dividing both sides of the above equation by $-2$, we get
$\Rightarrow m=-\dfrac{11}{2}$
Hence, the slope of the straight line is $-\dfrac{11}{2}$.
Using the points, we can also plot the graph of the line as follows

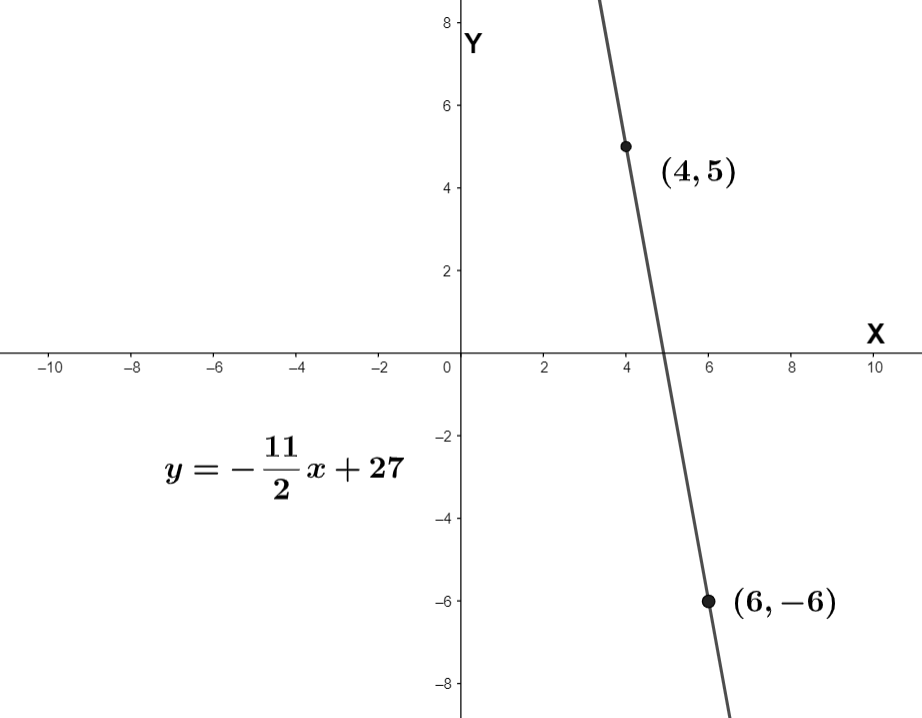
Note: We can also find the slope of the straight line using the formula,
$slope=\dfrac{\Delta y}{\Delta x}$
Using this formula here, we get

& \Rightarrow slope=\dfrac{-6-5}{6-4} \\\ & \therefore slope=-\dfrac{11}{2} \\\ \end{aligned}$$ Thus, we get the same answer from both of the above methods.