Question

How do you find the slope of the graph of $3x+5y=10$ ?

Answer 1

Here we can see we have to find the slope of the given equation.so, in order to find the slope of the given equation we have to first bring the equation in intercept form by rearranging. Then compare the given equation with the general intercept form of the equation which is $y=mx+c$ , here m is the slope and c is the intercept made by the line with y-axis.

Complete step by step answer:

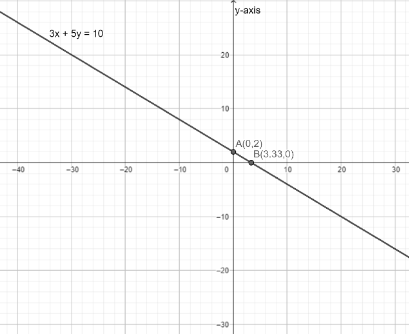
In the given question, the equation for which we have to find the slope is $3x+5y=10$. Let us first see what is slope and intercept. Slope is defined as the gradient of the line. In simple terms we can say the tangent of the angle made by the line with x-axis. It is just the change of over the change of . On the other hand, the intercept is the point where the line crosses the - axis. The distance from that intersection point to the origin is the value of intercept.
Now the equation given $3x+5y=10$ is not in general intercept form. Therefore, we will rearrange by shifting the x term to the right hand side and dividing by $5$ on both sides.

& 3x+5y=10 \\\ & \Rightarrow 5y=10-3x \\\ & \Rightarrow y=\dfrac{10}{5}-\dfrac{3x}{5} \\\ & \Rightarrow y=2-\dfrac{3}{5}x \\\ & \Rightarrow y=-\dfrac{3}{5}x+2 \\\ \end{aligned}$$ The equation after rearranging is $$y=-\dfrac{3}{5}x+2$$ . Comparing it with the general intercept form of the equation which is $$y=mx+c$$ . We get $$m=-\dfrac{3}{5}$$ . Hence, we can conclude that the slope of the given equation $$-\dfrac{3}{5}$$ is which means as the line on the graph moves from left to right, the line falls. **Note:** In this question the first step is to check whether the line is in intercept form or not. If it is not then you have to convert it into the general intercept form by rearranging. Also, while comparing the two equations do not leave the sign with it, be careful with this. The whole solution was dependent on the general intercept form of the equation so, try to memorize for future use also.