Question

How do you find the slope of the curve $f(x) = \sqrt {x - 1}$ at the point $x = 5$?

Answer 1

We need to find the slope of the curve $f(x)$ at the given point $x = a$. But, here the value of independent value is given as $x = 5$ and differentiate the function $f(x) = \sqrt {x - 1}$ as $f'(x)$ at the given point and plot a graph for the function and values.

Complete step by step solution:
Given,
The slope of a function $f(x) = \sqrt {x - 1}$ at the point $x = 5$.
To find a slope of curve,
By substitute point value into the function to art a graph,
To find curve at the point $(5,2)$ is mention below the following,

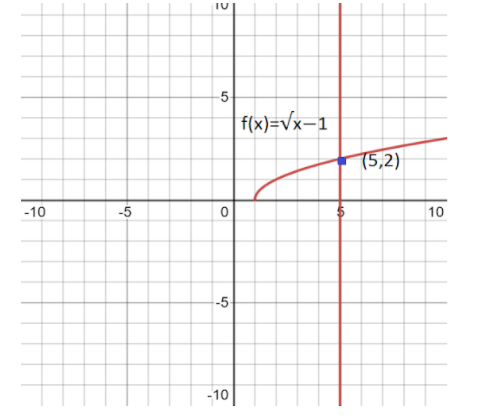
The slope of curve function $f(x) = \sqrt {x - 1}$……………..$(1)$
We have, the given Point at$x = 5$,
By take out the square root as power of $\dfrac{1}{2}$, we get
$f(x) = {(x - 1)^{1/2}}$
Differentiate the slope of function with respect to $x$, then we get
$f'(x) = \dfrac{1}{2}{(x - 1)^{\dfrac{1}{2} - 1}}$
By simplify the power fraction value, we get

To simplify, we get $$f'(x) = \dfrac{1}{2}{(x - 1)^{ - \dfrac{1}{2}}}$$ By write the power$$ - \dfrac{1}{2}$$ as fraction, we have $$f'(x) = \dfrac{1}{{2{{(x - 1)}^{\dfrac{1}{2}}}}}$$……………$$(2)$$ By substitute the point value$$x = 5$$ in the equation$$(2)$$, $$f'(5) = \dfrac{1}{{2{{(5 - 1)}^{\dfrac{1}{2}}}}}$$ By simplify the denominator value, we get $$f'(5) = \dfrac{1}{{2{{(4)}^{\dfrac{1}{2}}}}}$$ Put the power value by take square root, we get $$f'(5) = \dfrac{1}{{2\sqrt 4 }} = \dfrac{1}{{2\sqrt {2 \times 2} }}$$ By remove the square root to simplify, we get $$f'(5) = \dfrac{1}{{2 \times 2}} = \pm \dfrac{1}{4}$$ $$f'(5) = \pm \dfrac{1}{4}$$ Hence, the slope of the curve at the given value is $$ \pm \dfrac{1}{4}$$. **Note:** We need the slope of the curve function, $$f(x) = \sqrt {x - 1} $$ at the point of independent variable $$x = 5$$. By substitute the given values into the function and plot a graph with respect to the function and the point. We need to remember the concept to solve the problems with different values.