Question
Question: How do you find the slope of line \[x = 1\]?...
How do you find the slope of line x=1?
Solution
In the given question, we have been given an equation in two variables. We have to plot the line on a graph that forms from this equation. To do that, we first convert the given equation to slope-intercept form. From there, we find out the value of slope and the y-intercept. We plot a point at the y-intercept on the y-axis. From there, we move up or down and then right or left depending upon the coefficient of x and y respectively and join the points to form the line.
Formula Used:
The standard form of a linear equation in slope-intercept form is:
y=mx+b
Complete step by step answer:
The given equation is x=1.
We first convert this equation to the slope-intercept form,
y=mx+b
(0)y=(1)x−1
Hence, the slope of the line, m=1.
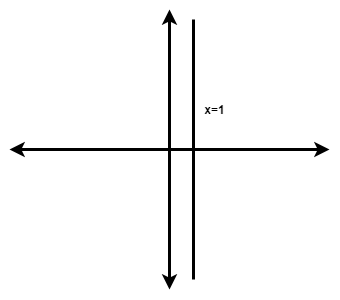
Now, clearly, this equation is an equation of a vertical line. In this vertical line, for each value of y, the corresponding value of x is 1.
Since x is never going to be zero, there is no y-intercept.
But we have x-intercept, (0,1).
Hence, we can graph it out like this:
Note:
In this question, we only need to know one thing – how to get the points for the graph and then, how to plot the points on the graph. Then we just calculate the values from the equation, plot them on the graph, join the points on the graph and we get the line that marks the required equation.
